- 自旋轨道耦合效应

自旋轨道耦合效应
背景
随着自旋电子学的迅猛发展,自旋轨道耦合效应越来越受到人们的广泛关注,国际上关于相关材料中自旋轨道耦合效应引起的各种新奇物理现象的报道越来越多,如自旋霍尔效应、自旋场效应晶体管、低损耗的自旋、自旋量子计算等。自旋轨道耦合作用提供了一种全电学(不需要外磁场或磁性材料)的方法控制自旋,随着理论研究的深入和实验技术的发展,基于自旋轨道耦合效应的各种电子器件层出不穷,也必将会带来更大的实际应用价值。
概念
自旋轨道耦合效应是指耦合电子的自旋自由度和它的轨道自由度之间的关系,这种关系提供了一种新的方式来控制电子自旋,即人们可以方便地用外加电场或门电压来控制和操纵电子的自旋,进而实现自旋电子器件。
自旋轨道耦合效应在半导体自旋电子学有很多具体应用,实际研究中根据介质材料所受力的性质和材料结构对称性可以将自旋轨道耦合效应分为Rashba自旋轨道耦合和Dressalhaus自旋轨道耦合。
Rashba自旋轨道耦合效应相互作用机制是由Rashba首先引入的,Rashba自旋轨道耦合起源于结构反演不对称,材料结构的非中心对称性将导致能带倾斜。
在三维晶体环境中,势能起源于晶体周期势。大多数多元半导体具有闪锌矿晶格结构或者铅锌矿晶格结构,二者都没有反演对称性。Dresselhaus证明了这种体反演不对称性质会导致导带有一个自旋轨道耦合引起的劈裂而形成两个子带。
起源
我们知道,电场对静止的电荷有静电力的作用,电场对运动的电荷除了有静电力的作用外还有磁场力的作用。磁场对静止的电荷没有力的作用,磁场对运动的电荷有力的作用。电场对静止磁矩无相互作用,电场对运动磁矩有力矩作用。自旋轨道耦合的本质是外电场对运动自旋磁矩的作用,自旋轨道耦合同时也是一个相对论的效应。
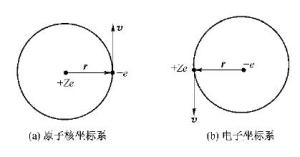 图1:两种不同坐标系示意图如图1中的额左图图(a)表示的是原子核坐标系,根据库仑定律,原子核在运动电子-e处产生一电场,电子绕原子核以速度v运动,存在一自旋磁矩,场对运动的磁矩将会产生相互作用,所以该自旋磁矩和由原子实在该处产生的电场将产生相互作用,这就是自旋轨道互作用的起源。由于运动是相对的,上述运动也可以看成电子不动,原子核绕电子运动,如图1中的右图图(b),对应的自旋轨道耦合则可以理解成电子是静止的,电场E以-v运动产生一个磁场B,这磁场B对自旋有力矩的作用。
图1:两种不同坐标系示意图如图1中的额左图图(a)表示的是原子核坐标系,根据库仑定律,原子核在运动电子-e处产生一电场,电子绕原子核以速度v运动,存在一自旋磁矩,场对运动的磁矩将会产生相互作用,所以该自旋磁矩和由原子实在该处产生的电场将产生相互作用,这就是自旋轨道互作用的起源。由于运动是相对的,上述运动也可以看成电子不动,原子核绕电子运动,如图1中的右图图(b),对应的自旋轨道耦合则可以理解成电子是静止的,电场E以-v运动产生一个磁场B,这磁场B对自旋有力矩的作用。
自旋是相对论量子力学的自然结果,所以更严格地给出原子中自旋轨道耦合必须要从狄拉克方程出发,通过狄拉克方程的非相对论极限可以得出自旋轨道耦合的具体形式。
相关研究
随着科技进步,很多由自旋轨道耦合所引起的新物理现象已被发现,并引起人们广泛的兴趣。特别是Mu-rakami和Sinova等人各自独立地预言了在自旋轨道耦合体系中,存在自旋霍尔效应。Sun等人预言了另一种由于自旋轨道耦合效应所引起的新的物理现象:在仅仅有自旋轨道耦合而无任何磁场、磁通的介观小环中,存在纯的持续自旋流。
Shi等人深入研究了自旋流的概念,提出了对自旋流新的定义,解决了自旋电子学领域的一个基本问题,对相关的后续研究有重要意义。自旋电子学的主要课题之一是自旋流的产生和有效控制。在金属和半导体中,导带电子的自旋轨道耦合可以有效的影响电子自旋状态,为调控电子自旋相干运动提供了一个有效的途径。最近,理论上提出了在空穴型半导体和半导体异质结的二维电子气中,由于自旋轨道耦合作用,外电场会产生一个切向的纯自旋流。这种内在的自旋霍尔效应已经成为一个广泛的研究课题。在过去,人们对电子自旋的研究主要集中在自旋与磁场的相互作用,很少有人考虑材料的体不对称性和面不对称性对自旋和轨道之间的相互作用的影响。有关介观输运方面的研究工作大多都以闪锌矿、纤维锌矿化合物半导体及其异质结构的基础上形成的二维电子气、量子线或量子点为对象。
Dresselhaus曾指出在这类缺乏体反演对称性的材料中,电子的自旋与轨道之间的相互作用能够引起半导体的能带劈裂,这种物理现象称为Dresselhaus自旋轨道耦合(spin-orbit interaction或者spin-orbit coupling)。Rashba自旋轨道耦合效应是由异质结结构反演非对称性引起的。尽管自旋轨道耦合作用的物理根源都来自于相对论效应,但它们对半导体能带结构的修正足以被实验观察到。自旋轨道耦合效应使在实空间运动的自旋电子感受到了等效磁场的作用,导致电子在运动中的自旋进动。在各种模型和器件中,对这种进动规律的研究可以给自旋注入和自旋控制提供新的思路。自旋轨道耦合使电子的自旋与运动相关联,从而可以通过控制电子的自旋来影响电子的运动,同时可以利用这种关联性来控制自旋的去相干和自旋驰豫。

-
江铃福特轻客持续打造最优TCO 锐骐超值版PK江铃国产共轨
2025-09-28 11:47:16 查看详情 -
新款冠道将于31日上市 45.98万元
2025-09-28 11:47:16 查看详情 -
雪佛兰星迈罗樱花限量版上市 广汽本田新款冠道正式上市
2025-09-28 11:47:16 查看详情 -
新款冠道将于31日上市 预售价119.8万元起/3排8座布局
2025-09-28 11:47:16 查看详情 -
V智电iDD上市 新款冠道将于31日上市
2025-09-28 11:47:16 查看详情 -
广汽本田新款冠道正式上市 售7.78万元起
2025-09-28 11:47:16 查看详情 -
比亚迪汉EV冠军版上市 新款冠道将于31日上市
2025-09-28 11:47:16 查看详情 -
广汽本田新款冠道正式上市 新款英菲尼迪QX50
2025-09-28 11:47:16 查看详情 -
成都本田冠道现金优惠达2.6万 成都广汽丰田逸致优惠2万元
2025-09-28 11:47:16 查看详情 -
新款冠道将于31日上市 款帝豪GL将于3月25日正式上市
2025-09-28 11:47:16 查看详情


 求购
求购

