- 轴矢量

轴矢量
简介
轴矢量是指在镜面对称变换下法分量不变而切分量改变的矢量(宇称为正的矢量),它是相对于极矢量而言的概念。矢量作为有方向的量,在坐标转动时,分量随坐标作相应变化。极矢量在宇称变换(空间完全反演)下,大小不变,方向变得相反。轴矢量在宇称变换下方向不改变。最常见的轴矢量,是角速度、角动量和磁感应强度[1]。
定义公式
设有一矢量![]() 在关于平面
在关于平面![]() 的镜面反射变换
的镜面反射变换![]() 下满足
下满足
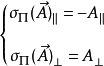
则称矢量![]() 为轴矢量[1]。
为轴矢量[1]。
(![]() 与
与![]() 分别是
分别是![]() 关于平面
关于平面![]() 平行和垂直的分量)
平行和垂直的分量)
轴矢量的经典物理解释
矢量作为有方向的量,在坐标转动时,分量随坐标作相应变化。极矢量在宇称变换(空间完全反演)下,大小不变,方向变得相反。轴矢量在宇称变换下方向不改变。最常见的轴矢量,是角速度、角动量和磁感应强度[1]。它们与极矢量不同的一个明显例子如下:一般而言,一个垂直镜子的物体,在镜子里的像方向与自己相反;而一个转轴与镜子垂直的螺旋,在镜子里的像的旋转方向跟实物的旋转方向一样,标志其旋转方向的矢量(角速度)也与实物的角速度方向相同。
一般而言,两个极矢量的外积是轴矢量。
轴矢量的粒子物理解释
在粒子物理里,既有矢量性质的流,又有轴矢量性质的流。特别重要的一个例子是弱相互作用相关的流,正好是矢量流和轴矢流之和。这样的流由于既含有宇称为正的部分又含有宇称为负的部分,因此总的宇称是不守恒的。这正是在弱相互作用下宇称不守恒的根源。虽然流守恒的特性上,轴矢量流和矢量流并没有什么不一样,但是在自然界中,矢量流是更为根本的。不仅除弱相互作用外的其他相互作用都是与矢量流相关的,而且在量子的层面上,轴矢流有矢量流完全没有的性质--量子反常。
极矢量和轴矢量的判别
在垂直于所讨论的矢量平面内得到该矢量在平面镜中的像,若该矢量的镜像和原有矢量的方向相反,则此矢量是极矢量。如质点的位移矢量,在垂直于位移矢量的平面镜内看到质点的位移方向与原矢量方向相反,故位移矢量是极矢量。同样可判别力、速度、加速度、动量、冲量、电场强度 等为极矢量。若所讨论的矢量的镜像与原有矢量方向相同,则此矢量是轴矢量。如绕固定轴转动的刚体的角速度矢量,在垂直于角速度的平面镜内看到刚体的镜像,其角速度 仍按原方向旋转,其矢量的镜像方向与原矢量方向一致,,故角速度是轴矢量。采用同样的方法可判别力矩、角动量、角加速度等为轴矢量。
刀轴矢量的控制方式
刀轴矢量的控制方式在多轴数控加工中非常重要,它决定了刀具与被加工表面之间是否产生干涉、相邻刀轴是否平稳变化、机床实际加工时能否超程和刀具的有效加工空间等等。对于CAM软件中提供的各种倾斜方式,必须根据不同的加工特征合理的进行选择,才能达到理想的加工效果。常用的几种倾斜方式有沿切削方向倾斜、过点倾斜、过曲线倾斜,而不倾斜且与曲面垂直这种方式多用于定位加工。通过设置前倾角和侧倾角、合理选择空间点的坐标和曲线的方程可获得非干涉刀轴矢量,最后利用CAM软件中自带的仿真功能进行模拟验证。

-
超宽带矢量信号发生器
2025-09-20 08:47:54 查看详情 -
PSG矢量信号发生器
2025-09-20 08:47:54 查看详情


 求购
求购










