循环数

最广为人知的循环数是142857.其循环如下：

142857 × 1 = 142857

142857 × 2 = 285714

142857 × 3 = 428571

142857 × 4 = 571428

142857 × 5 = 714285

142857 × 6 = 857142

为了确认一个数是否是循环数，需要保证这个数是乘连续的若干个数后发生循环。因此，076923不会被认为是一个循环数，即使它各位循环后的数都是它的倍数。

以下这些数比如是循环数；

1、单独的一位数，如5

2、单位重复的数，如555

3、循环数的重复，如142857

如果前导0不被允许，142857将是唯一一个十进制循环数。如果允许前导0，前几个循环数是：

142857 (6位)

0588235294117647 (16位)

052631578947368421 (18位)

0434782608695652173913 (22位)

0344827586206896551724137931 (28位)

0212765957446808510638297872340425531914893617 (46位)

0169491525423728813559322033898305084745762711864406779661 (58位)

016393442622950819672131147540983606557377049180327868852459 (60位)

循环数与单位分数的循环小数表示形式有关。一个长为L的循环数在数字上是1/(L+1)的循环节。相反的，如果1/p(p是质数）的循环节长度为p-1，它的循环节在数字上就是一个循环数。

由循环数与单位分数的关系可得，循环数有这样的形式

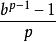
其中b是数基（对于十进制，b=10），而p是一个不是b的倍数的质数（能产生循环数的质数被称为全循环质数）

例如，b=10,p=7时会产生142857.

不是所有的p会根据这个公式产生循环数。例如当p=23时会产生076923076923。这些失败的例子总包含重复的数。

前几个产生十进制循环数的质数包括（OEIS中的数列编号为A001913）

7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983 …

这个数列中所有的数p满足10是p的模p原根，Emil Artin猜想称37.395..%的质数属于这个数列。^[1]

循环数可以用程序构造，伪代码如下（其中b,p的定义上文已给出）

t = 0.

r = 1.

n = 0.

loop:

t = t + 1

x = r * b

d = int(x / p)

r = x mod p

n = n · b + d

If r ≠ 1 then goto loop;

if t = p - 1 then n is a cyclic number.

这个程序通过使用长除法计算1/p的数位构造。r是每一步的余数，d是产生的数。

若 t > p/2, 则这个数必定为循环数, 无需继续计算后面部分了。

乘以产生一个循环数的质数时，结果会是一系列的9.如 142857 × 7 = 999999。

如果将其按位划分成若干等长份并加在一起，结果会是一系列的9.这是Midy定理的特殊情况。如14 + 28 + 57 = 99 142 + 857 = 999 1428 + 5714+ 2857 = 9999

所有的循环数都是9的倍数。^[2]

二进制

01

0011

0001011101

000100111011

000011010111100101

三进制

0121

010212

0011202122110201

001102100221120122

0002210102011122200121202111

八进制

25

1463

0564272135

0215173454106475626043236713

0115220717545336140465103476625570602324416373126743

十二进制

2497

186A35

08579214B36429A7

二十四进制

3A6LDH

248HAMKF6D

1L795CN3GEJB

19M45FCGNE2KJ8B7

可以证明当 b 为完全平方数时，不存在长度超过1的循环数。