联合概率分布

根据随机变量的不同，联合概率分布的表示形式也不同。对于离散型随机变量，联合概率分布可以以列表的形式表示，也可以以函数的形式表示；对于连续型随机变量，联合概率分布通过非负函数的积分表示。^[1]

给定样本空间，其上的实值函数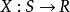称为（实值）随机变量。

如果随机变量X的取值是有限的或者是可数无穷尽的值，则称X为离散随机变量。

如果X是由全部实数或者由一部分区间组成，则称X为连续随机变量，连续随机变量的值是不可数及无穷尽的。

随机变量分为离散型随机变量和连续型随机变量，当要求随机变量的概率分布的时候，要分别处理。^[2]

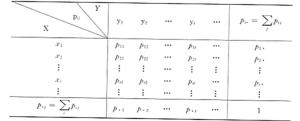
对于二维离散随机向量，设X和Y都是离散型随机变量，和分别是X和Y的一切可能的集合，则X和Y的联合概率分布可以表示为如右图的列联表，也可以表示为如下的函数形式：^[3]

其中

多维随机变量的中，只包含部分变量的概率分布称为边缘分布：

对于多维（维数大于等于3）离散型随机变量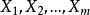的联合概率分布以此类推。

对于二维连续随机向量，设X和Y为连续型随机变量，其联合概率分布，或连续型随机变量的概率分布通过一非负函数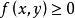的积分表示，称函数为联合概率密度。^[3]

两者的关系如下：

不但完全决定X和Y的联合概率分布，而且完全决定X的概率分布和Y的概率分布，以和分别表示X和Y的概率密度，则

对于多维（维数大于等于3）连续型随机变量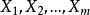的联合概率分布以此类推。