- 变形椭圆

变形椭圆
概念
假设考虑地面(地球椭球体面)是一个微小的无穷小圆(称微分圆),在投影中发生变形后,往往不能保持为圆形,而是一个椭圆,称为变形椭圆。根据变形椭圆的形状和大小,能反映出投影中变形的质和量的差别,同时具有直观的明晰形。如在等角投影中,变形椭圆保持正圆形,但在不同的位置上,面积差异很大,而在等积投影中,则变形椭圆形状变化很大,但面积大小相等。
基本原理
两个全等椭圆相滚动,如图1中![]() 、
、![]() 及图2中
及图2中![]() 、
、![]() ,其传动比
,其传动比![]() 作对称变化,如图3中
作对称变化,如图3中![]() ;而两个变形椭圆相滚动,如图2中的
;而两个变形椭圆相滚动,如图2中的![]() 、
、![]() ,传动比则可作不对称变化,如图3中的
,传动比则可作不对称变化,如图3中的![]() 。
。
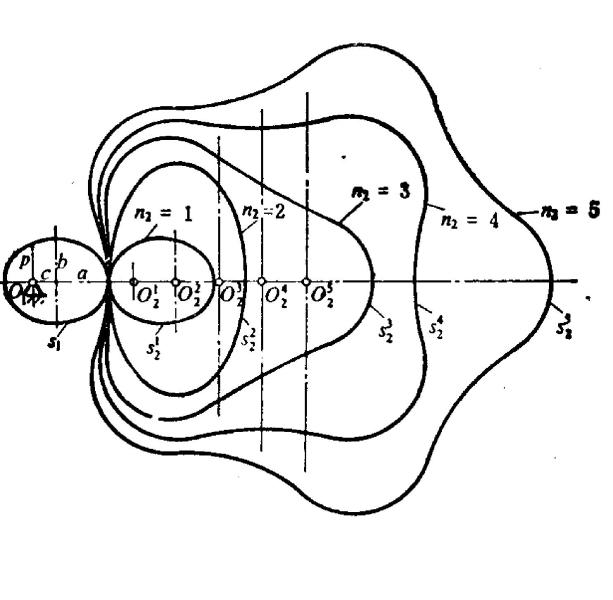 图1
图1
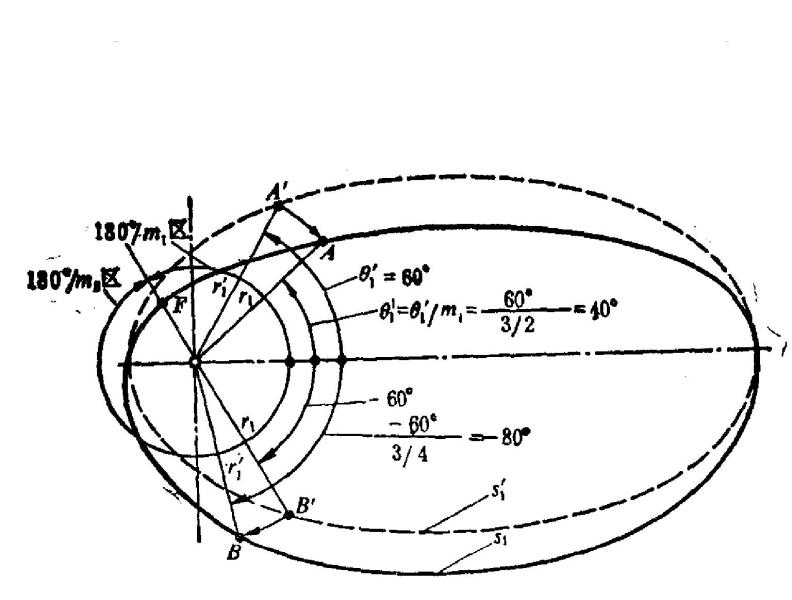 图2
图2
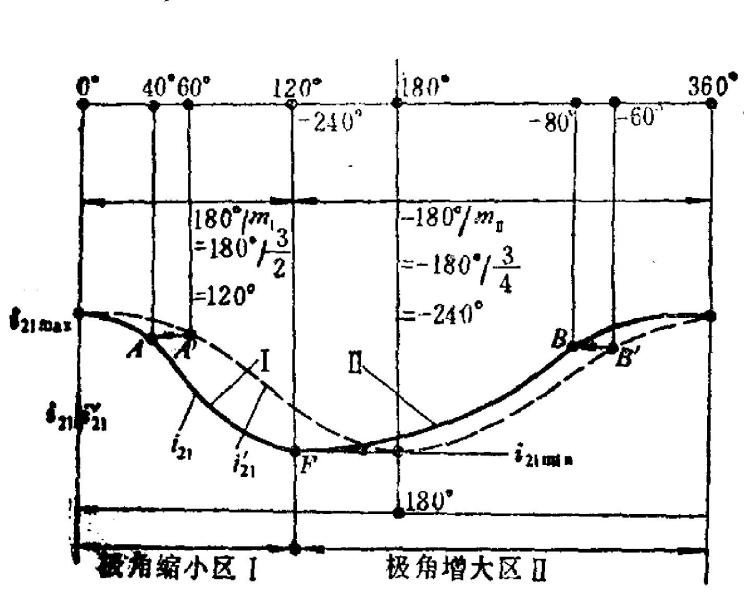 图3
图3
图2表示如何由原始椭圆![]() 导出称为变形椭圆的
导出称为变形椭圆的![]() 。图中两椭圆极径
。图中两椭圆极径![]() 相同而极角
相同而极角![]() 则不同。在极角缩小区内,极角缩小系数
则不同。在极角缩小区内,极角缩小系数![]() ,缩小区域占
,缩小区域占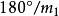 ,例如图2中
,例如图2中![]() 上点
上点![]() 处极角
处极角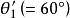 缩小成
缩小成![]() 上点
上点![]() 的极角
的极角![]()
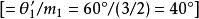 ,但点
,但点![]() 、
、![]() 处的极径
处的极径![]() 不变,这样
不变,这样![]() 、
、![]() 相应的极径
相应的极径![]() 不变,图3中的
不变,图3中的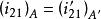 亦不变。在极角增大区内,极角增大系数
亦不变。在极角增大区内,极角增大系数![]() ,增大区域占
,增大区域占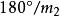 ,例如图2中的
,例如图2中的![]() 上点
上点![]() 的极角
的极角![]() (“
(“![]() ”号仅表反向量度)增大为
”号仅表反向量度)增大为![]() 上点
上点![]() 的极角
的极角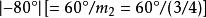 ,但点
,但点![]() 、
、![]() 处的极径
处的极径![]() 不变,这样
不变,这样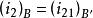 亦不变(见图3)。变形椭圆
亦不变(见图3)。变形椭圆![]() (图2)及其不对称的传动比
(图2)及其不对称的传动比![]() (图3)就是基于这种方法由原始椭圆
(图3)就是基于这种方法由原始椭圆![]() 推导出来的。上述
推导出来的。上述![]() 、
、![]() 要满足
要满足
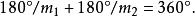
从图3可知,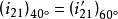 ,所以只要将用于原始椭圆
,所以只要将用于原始椭圆![]() 中的
中的![]() 用
用![]() 代入即得变形椭圆
代入即得变形椭圆![]() 在
在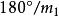 区
区![]() 处的传动比
处的传动比![]() 。[1]
。[1]

相关百科
-
极速创建:3ds Max/VRay变形金刚与场景
2025-09-21 05:55:25 查看详情 -
变形金刚中大黄蜂是什么车型?
2025-09-21 05:55:25 查看详情 -
变形金刚中有雪佛兰的哪些车型(一二部)
2025-09-21 05:55:25 查看详情 -
为什么变形金刚中的车牌子是雪佛兰。???
2025-09-21 05:55:25 查看详情 -
变形铝及铝合金化学成分
2025-09-21 05:55:25 查看详情


 求购
求购






