- 决策表

决策表
定义
用表格的方式描述决策问题一种方法,这种表格也被称为决策矩阵。所谓决策表是指一个以行、列形式来描述和表示决策规则和知识信息的表,如果决策问题的后果是用损失的费用表示,这个表也被称为损失矩阵。
表示
决策表的一般表示如下表。
在决策表中,表示可供选择的决策行为,;表示决策行为实施之后的自然状态,而表示实施选择决策 ai后,自然状态是 θi的决策后果,人们有时喜欢使用这个矩阵的转置形式。
上述的决策表可以更加一般化,一方面,决策结果的自然状态可能是无限的、具有一定的相容性或者不可直接观察性等等变化; 另一方面,决策后果可能具有更加一般的信息含义,例如: 用效用函数衡量,而后果的出现并不单单是以概率方式描述,具有更为一般的不确定性性质等等。具体的使用,可以根据实际情况加以灵活运用。[1]
结构
决策表一般分为4个部分,见下图。 每个条件对应一个变量、关系或预测,“候选条件”就是它们所有可能的值;动作指要执行的过程或操作;动作入口指根据该入口所对应的候选条件集,是否或按怎样的顺序执行动作。 许多决策表在候选条件中使用“不关心”符号来化简决策表,尤其是当某一条件对应要执行的动作影响很小时。有时,所有的条件在开始时都被认为是重要的,但最后却发现没有一个条件对执行的动作有影响,都是无关的条件。
在这4个部分的基础上,决策表根据候选条件和动作入口的表现方法的变化而变化。有些决策表使用true/false作为候选条件值(类似与if-then-else),有些使用数字(类似于switch-case),有些甚至使用模糊值或概率值。对应动作入口,可以简单的表示为动作是否执行(检查动作执行),或更高级些,罗列出要执行的动作(为执行的动作排序)。
示例
有限决策表(Limited-entry Decision Table)是最简单的一个形式。候选条件为布尔值,动作入口为X符号,表示在某一列中哪个动作将被执行。
一个技术支持公司用一个决策表,根据用户通过电话向他们描述的问题症状,来诊断打印机的故障所在。
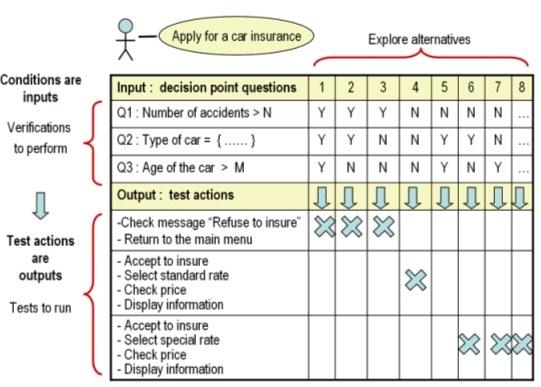 图1.决策表
图1.决策表
当然,这只是一个简单的例子(表中的动作也不一定符合现实情况),但是从这个表中可以看出,根据可能的情况随着条件的数量的增加而增加。在这个例子中有3个条件,可能的组合是8个。
优点
决策表能罗列出所有的可能情况,并清晰的指出相应的处理方式,用户不需要考虑其中的逻辑关系就能一眼看出其中什么样的动作对应什么样的情况,这比程序语言中层层嵌套的逻辑语句要强多了。而所有可能情况的平面罗列,也能避免在程序语言编写中,因为逻辑上的层层嵌套而产生遗漏,尤其在if-then-else结构中else部分是可选的情况下。
因为逻辑控制在编程中的重要地位,决策表成为设计逻辑控制时十分重要的一个工具。

-
长城官方针对拖车钩断裂事件发表声明 进一步开拓海外市场
2025-01-27 08:43:38 查看详情 -
比亚迪新款唐EV将于今日上市 全液晶仪表+可旋转中控屏
2025-01-27 08:43:38 查看详情 -
新款比亚迪汉EV实车图曝光 全液晶仪表+可旋转中控屏
2025-01-27 08:43:38 查看详情


 求购
求购







