十字链表

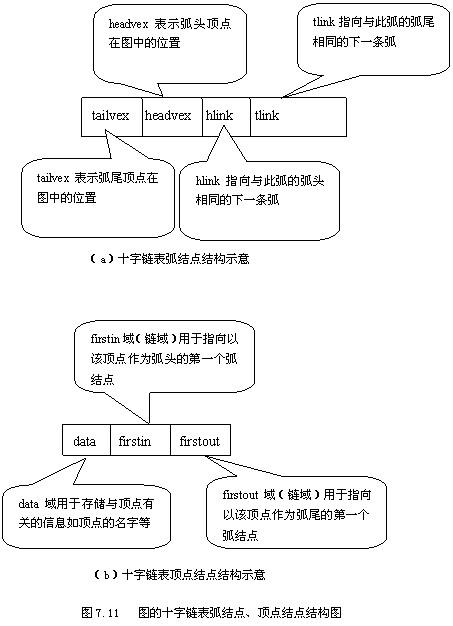示意图十字链表(Orthogonal List)是有向图的另一种链式存储结构。我们也可以把它看成是将有向图的邻接表和逆邻接表结合起来形成的一种链表。有向图中的每一条弧对应十字链表中的一个弧结点，同时有向图中的每个顶点在十字链表中对应有一个结点，叫做顶点结点。这两类结点结构如图所示。

例如：图G的十字链表表示如图7.12所示。若有向图是稀疏图，则它的邻接矩阵一定是稀疏矩阵，这时该图的十字链表表示法可以看成是其邻接矩阵的链表表示法。只是在图的十字链表表示法中，弧结点所在的链表不是循环链表且结点之间相对位置自然形成，不一定按顶点序号有序。另外，表头结点即顶点结点，它们之间并非循环链式连接，而是顺序存储。 

图的十字链表结构形式化定义如下：图7.12

#define MAX_VERTEX_NUM 10 
 /*最多顶点个数*/
typedef  enum{DG, DN, UDG, UDN} 
GraphKind;  /*图的种类*/
 typedef  struct ArcNode {
 int  tailvex,  headvex; 
   struct ArcNode *hlink, *tlink;   
} 
ArcNode;
typedef struct VertexNode {
   VertexData   data;    /*顶点信息*/
   ArcNode    *firstin,  *firstout;  
}
VertexNode;
typedef struct {
   VertexNode   vertex[MAX_VERTEX_NUM];  
   int  vexnum,  arcnum;   /*图的顶点数和弧数*/
   GraphKind   kind;              /*图的种类*/
} 
OrthList;      /*图的十字链表表示法(Orthogonal List)*/
//建立一个有向图的十字链表的算法如下：
void  CrtOrthList（OrthList  *g）
/*从终端输入n个顶点的信息和e条弧的信息，以建立一个有向图的十字链表*/
{
scanf(“%d,%d”,&n,&e);  /*从键盘输入图的顶点个数和弧的个数*/
for (i=0;i<n;i++)
   {scanf(“%c”,&g->vertex[i].data）；
   g.vertex[i] .firstin=NULL；g.vertex[i] .firsout=NULL；
   }
for (k=0;k<e;k++)
   {scanf(“%c,%c”,&vt,&vh);
    i=LocateVertex（g，vt）；j = LocateVertex（g，vh）；
    p=( ArcNode*)malloc(sizeof(ArcNode));
    p->tailvex=i；p->headvex=j；
    p->tlink = g->vertex[i].firstout；g->vertex[i].firstout =p；
    p->hlink = g->vertex[j].firstin；g->vertex[j].firstin =p；
    }
}
/* CrtOrthList */

                算法 7.2  创建图的十字链表

在十字链表中既能够很容易地找到以vi为尾的弧，也能够容易地找到以vi为头的弧，因此对于有向图，若采用十字链表作为存储结构，则很容易求出顶点vi的度。此外，为有向图建立一个邻接表和建立一个十字链表的算法的时间复杂度是相同的。所以，在某些有向图的应用中，十字链表表示法得到了广泛地应用。

十字链表的构成　　

用链表模拟矩阵的行（或者列，这可以根据个人喜好来定），然后，再构造代表列的链表，将每一行中的元素节点插入到对应的列中去。十字链表的逻辑结构就像是一个围棋盘（没见过，你就想一下苍蝇拍，这个总见过吧），而非零元就好像是在棋盘上放的棋子，总共占的空间就是，确定那些线的表头节点和那些棋子代表的非零元节点。最后，我们用一个指针指向这个棋盘，这个指针就代表了这个稀疏矩阵。  

链表（Orthogonal List)是有向图的另一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中，对应于有向图中每一条弧都有一个结点，对应于每个定顶点也有一个结点。

#include < malloc.h>
#include /*十字 链表的 结构类型定义如下：*/
typedef struct OLNode
{
int row,col; /*非零元素的行和列下标*/
ElementType value;
struct OLNode *right; /*非零元素所在行表、列表的后继链域*/
struct OLNode *down;
}
OLNode; *OLink;
typedef struct
{
OLink *row_head; /*行、列链表的头指针向量*/
OLink *col_head;
int m,n,len; /*稀疏矩阵的行数、列数、非零元素的个数*/
}
CrossList; /*建立稀疏矩阵的十字链表的算法*/
void CreateCrossList(CrossList *M)
{             /*采用十字链表存储结构，创建稀疏矩阵M*/
　　scanf(&m,&n,&t); /*输入M的行数,列数和非零元素的个数*/
　　M->m=m;
　　M->n=n;
　　M->len=t;
　　if(!(M->row_head=(OLink *)malloc((m+1)sizeof(OLink))))
　　exit(OVERFLOW);
　　if(!(M->col_head=(OLink * )malloc((n+1)sizeof(OLink))))
　　exit(OVERFLOW);
　　M->row_head[ ]=M->col_head[ ]=NULL; /*初始化行、列头指针向量，各行、列链表为空的链表*/
　　for(scanf(&i,&j,&e);i!=0;scanf(&i,&j,&e))
　　{
　　if(!(p=(OLNode *)malloc(sizeof(OLNode))))
　　exit(OVERFLOW);
　　p->row=i;
　　p->col=j;
　　p->value=e; /*生成结点*/
　　if(M->row_head==NULL)
　　M->row_head=p;
　　else
　　{
　　/*寻找行表中的插入位置*/
　　for(q=M->row_head;q->right&&q->right->col<j;q=q->right); /*空循环体*/
　　p->right=q->right;
　　q->right=p; /*完成插入*/
　　}
　　if(M->col_head[j]==NULL)
　　M->col_head[j]=p;
　　else
　　{
　　/*寻找列表中的插入位置*/
　  for(q=M->col_head[j];q->down&&q->down->row<i;q=q->down); /*空循环体*/
　　p->down=q->down;
　　q->down=p; /*完成插入*/