磁滞损失

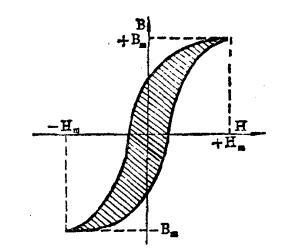磁滞回线交变磁通在铁芯中不但引起涡流损失，同时还要产生磁滞损失。铁芯在磁化和去磁的过程中，有磁滞现象。在交流磁路中，磁场强度H的大小与方向不断地变化，铁芯被反复地磁化和去磁。在这个过程中，外磁场不断地驱使磁畴转向，就需要克服磁畴间的阻碍作用而消耗能量。这种能量的损耗就叫做磁滞损失。实验和数学分析都可以证明，在单位体积的铁芯中所产生的磁滞损失，与磁滞回线的面积（图中磁滞回线所包围的阴影部分）成正比。所以，磁滞回线所包围的面积愈大，磁滞损失就愈大。励磁电流的频率愈高，即单位时间内磁场强度H所完成的循环次数愈多，磁滞损失也愈大。当频率一定时，磁滞损失大致上与磁感应强度最大值的平方成正比。

由此可见，交流励磁的磁路应尽量采用磁滞回线狭小的软磁材料，如硅钢等。在电子和高频方面用的高频元件采用铁氧体等软磁材料，可以减少磁滞损失。

交变磁通在铁芯中所产生的涡流损失和磁滞损失加起来叫做铁芯损失，简称铁损砸ΔP_Fe，这两种损失都要从电源吸取能量，并转化为热能而使铁芯发热。因此，在设计大容量的交流发电机、变压器和电动机时，要计算铁芯发热的情况，并采取各种相应的冷却措施，如风冷、油冷、水冷等。在运行过程中，要注意监视铁芯的温度，以防过热。电工设备的铁损可以用试验的方法测出。

铁芯线圈的简化相量图是没有考虑铁芯中能量损失画出来的。那么，铁芯中的磁滞和涡流损失的存在，对于铁芯线圈电路的相量图会有什么样的影响呢?为了供给铁芯损失所需要的能量，线圈必须从电源吸取有功功率。也就是说，即使不考虑线圈电阻所消耗的功率，线圈吸取的有功功率也不再等于零而应等于铁损。即

P = VIcosφ=ΔP_Fe

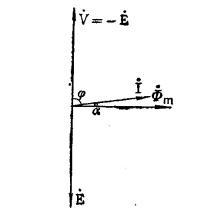考虑铁损时铁芯线圈电路的相量图因此，铁芯线圈的功率因数不等于零，而应该是cosφ= ΔP_Fe/VI，电压与电流之间的相位差φ必定小予90°，而大于0°，即0°<φ<90°。

这时，电流I应比Φ_m越前α角。这样，铁芯线圈电路的相量图就如图所示。可见如果考虑铁损，励磁电流和主磁通就不同相了。铁芯损失愈大，α角也愈大，所以α角叫做铁内损失角。^[1]

磁滞损失的产生，是由于铁心在磁化过程与去磁过程中，在B-H曲线上以不同的路线进行，这一路线曲线就称为磁滞回线。在这种情况下不仅磁路所需的瞬时功率不为0，而且平均功率也不等于0。磁滞损耗的能量转换为热能而使铁心发热。

交变磁通在铁芯中不但引起涡流损失，同时要引起磁滞损失。磁滞损失用ΔP_z表示。

为什么会引起磁滞损失呢?前面在分析磁滞影响使基波电流和线圈两端电压之间相位差小于π/2的情况时已作了简单说明。现在从磁化角度出发再说明一下原因。铁芯在交变磁化的过程中，磁性材料磁畴不停地改变方向，磁畴之间会产生相互摩擦现象而使铁芯发热，所以要消耗能量。

实验和数学分析可以证明，计算磁滞损失时常用下面的经验公式，即

ΔP_z= δ_zfB_m^[2]

铁磁质的剩磁现象

铁磁材料除了具有高的磁导率外，另一重要的磁性特点就是磁滞。设铁磁性材料已沿起始磁化曲线磁化到饱和，磁化开始饱和时的磁感应强度值用表示。如果在达到饱和状态之后使H减小，这时B的值也要减小，但不沿原来的曲线下降，而是沿着上一条曲线段下降，对应的值比原先的值大，说明铁磁质磁化过程是不可逆的过程。当 H=0时，B不为零，而是大于零，称为剩余磁感应强度，简称剩磁，这是铁磁质的剩磁现象。

要消除剩磁，使铁磁质中的恢复为零，需加反向磁场，反向磁场强度称为矫顽力。继续增加反向磁场 。材料又可被反向磁化达到反方向的饱和状态，以后再逐渐减小反方向的磁场至零值时，和的关系将沿左下段变化，这时改变线圈中的电流方向，即又引入正向磁场。当磁场强度变化一个周期后，铁磁质的磁化曲线形成一个闭合曲线。

磁滞现象

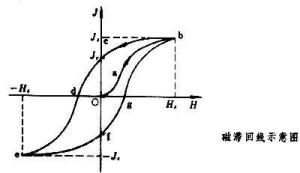磁滞回线磁感应强度值的变化总是落后于磁场强度的变化，这种现象称为磁滞，是铁磁质的重要特性之一，上述闭合曲线常称为磁滞回线。各种不同的铁磁性材料有不同的磁滞回线，主要是磁滞回线的宽、窄不同和矫顽力的大小有别。磁滞回线是介质内部磁场强度和磁感应强度的关系曲线。 一般说来，铁磁体等强磁物质的磁化强度M或磁感应强度B，不是磁场强度H的单值函数而依赖于其所经历的磁状态的历史。以磁中性状态（H =M=B=0）为起始态,当磁状态沿起始磁化曲线0ABC磁化到 C点附近（如图）时，此时磁化强度趋于饱和，曲线几乎与H轴平行。将此时磁场强度记为H_s，磁化强度记为M_s。此后若减小磁场，则从某一磁场（B点）开始，M随H的变化偏离原先的起始磁化曲线，M的变化落后于H。当H 减小至零时，M不减小到零，而等于剩余磁化强度M_r。为使M减至零，需加一反向磁场，称为矫顽力。反向磁场继续增大到-H_s时，强磁体的M将沿反方向磁化到趋于饱和-M_s，反向磁场减小并再反向时，按相似的规律得到另一支偏离反向起始磁化曲线的曲线。于是当磁场从Hs变为-H_s，再从-H_s变到H_s时，强磁体的磁状态将由闭合回线CBDEFEGBC描述，其中BC及EF两段相应于可逆磁化，M为H的单值函数。而BDEGB为磁滞回线。在此回线上，同一H可有两个M值，决定于磁状态的历史。这是由不可逆磁化过程所致。若在小于H_s的±H_m间反复磁化时，则得到较小的磁滞回线。称为小磁滞回线或局部磁滞回线（见磁化曲线图）。相应于不同的H_m，可有不同的小回线。而上述 BDEGB为其中最大的。故称为极限磁滞回线。H大于极限回线的最大磁场强度H_s时，磁化基本可逆；H小于此值时，M为H的多值函数。通常将极限磁滞回线上的Mr及定义为材料的剩磁及矫顽力，为表征该材料的磁特性的重要参量。^[3]