对数平均温差

先假设有一个泛用的热交换器，其二端（称为A及B）分别有热蒸气及冷蒸气进出，对数平均温差定义为以下的对数平均：

其中

ΔT_A是热蒸气及冷蒸气在A端的温度差。

ΔT_B是热蒸气及冷蒸气在B端的温度差。

依此定义，LMTD可以用来推算热交换器所传递的热

其中

Q是传递的热（单位 J）

U为传热系数（单位 J/ K m²）

Ar为热交换面积

不过传热系数的估算可能相当的复杂。

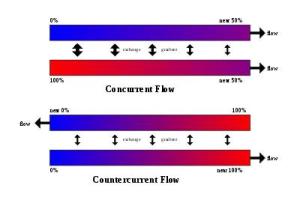热交换器的并流（Concurrent）及逆流（countercurrent）

若热交换器是并流（热蒸气及冷蒸气平行，都从某一侧进，从另一侧出）或是逆流（热蒸气及冷蒸气平行，但各由一侧进，从另一侧出），以上的式子都会成立。

若是交叉流（cross-flow）热交换器，也就是热交换器中有散热片，上面的温度接近定值，其热交换量和LMTD也会有类似的关系，不过会出现修正系数。若是结构比较复杂的热交换器（例如壳管式热交换器），也会有修正系数。

假设热传导是在沿着z轴上，从A点到B点的热交换器上进行，热传导是在二种流体之间交换能量，分别标示为1和2，沿着z轴的热量分别是T₁(z)和 T₂(z)。

沿着z上的局部交换热通量和其温度差成正比：

其中D为二流体之间的距离。

流体释放的热会依傅立叶定律产生温度梯度：

相加后，可得

where K=k_a+k_b.

交换的总能量可以由A点到B点的局部热交换量q积分而得：

热交换面积Ar为管长A-B乘以二管间的距离D：

二个积分都作变数变换，积分变数由z改为Δ T：

配合上述Δ T的关系，可得：

积分的结果如下：

,

也就是对数平均温差的定义。

假设二流体温度的变化率和其温差成正比，这对固定比热的流体有效，流体的温度变化若在一个较小的范围，此假设成立，不过若比热有变化，用计算对数平均温差计算的热交换量就不准了。

LMTD不适用在冷凝器及再沸器中，其中包括了相变化及其潜热，因此假设无效。

假设热传系数U为定值，和温度无关，若热传系数和温度有关，计算的准确度也会下降。

LMTD是一个稳态的概念，不适用在暂态的分析。特别若LMTD应用在暂态中，其时间较短，热交换器的二边温度梯度的符号相反，对数的引数会出现负值，这也是不允许的。