- 投票制度

投票制度
介绍
投票制度规定了选民表达民意的方式,以及把这些民意转化成结果的方法。研究投票制度的学问被称为“投票理论”,始于18世纪,对各种投票制度提出严谨定义和改良建议,属于政治学、经济学、和数学的子学科。
投票制度观点
投票制度会详细规定“选票”的形式,以及计算投票结果的算法。投票结果可能是单一候选人获胜,也可能是多人获胜,如立法机构的选举。投票制度也会表明选民的投票权如何分配,以及选民如何被分配到独立的选区。
选举的实际操作通常并不是投票制度关心的课题。投票制度不会指明选票是用纸张制成,或用打卡票,或是电子投票。投票制度也不会指明如何保护选民隐私、如何正确地计算选票、或谁拥有投票权。这些是属于更广泛的选举或选举制度的研究范围。
选票
 在简单的多数制里,投票者只能选择一个项目不同投票制度有不同形式的选票。在次序投票制里,如同排序复选制和波达计数法(Borda Count),选民根据支持程度将选项排序。而在计分投票制(Range voting)里,选民则给每个选项评分。在多数制(也被称为“最高票者当选制”)中,选民只能选择一个项目;而在认可投票制里,选民可以选择任何候选项目;在与能投票制中,选民可以在选票上圈选多个候选项目。其中,可圈选的项数,可依据不同民情而设定不同计算公式。而在累积选举制里,选民可以投给同一个候选人许多票。
在简单的多数制里,投票者只能选择一个项目不同投票制度有不同形式的选票。在次序投票制里,如同排序复选制和波达计数法(Borda Count),选民根据支持程度将选项排序。而在计分投票制(Range voting)里,选民则给每个选项评分。在多数制(也被称为“最高票者当选制”)中,选民只能选择一个项目;而在认可投票制里,选民可以选择任何候选项目;在与能投票制中,选民可以在选票上圈选多个候选项目。其中,可圈选的项数,可依据不同民情而设定不同计算公式。而在累积选举制里,选民可以投给同一个候选人许多票。
其他投票制度的选票还有其他安排,例如选民可以写下候选人的姓名,或者选民可以否决所有选项(如果成立,则选举就必须从提名阶段重新进行)。
选票的份量
许多选举以“一人一票”的概念进行,即每名选民的选票有相同价值。然而,例如在公司的选举里,选票的价值通常依据投票者所持有的公司股份计算,变成“一股份一选票”。
 美国参议院在部分选举中,选票的价值因应投票者的地位而定。而在特殊情况下,例如投票平手时,其中一名投票者获特权再投一票以决定胜负。拥有这种特权的投票者可能原先并没有投票权,例如美国参议院中,美国副总统一般情况下没有投票权,他只能在议会投票平手时,才可以投票,所以实际上他那一票的价值是较一般选票为少。
美国参议院在部分选举中,选票的价值因应投票者的地位而定。而在特殊情况下,例如投票平手时,其中一名投票者获特权再投一票以决定胜负。拥有这种特权的投票者可能原先并没有投票权,例如美国参议院中,美国副总统一般情况下没有投票权,他只能在议会投票平手时,才可以投票,所以实际上他那一票的价值是较一般选票为少。
选票份量和选票动员力是不同的,因为每名人士不一定是各自独立行事,他们往往会组织起来共同投票。动员力高的投票团体,其成员投票选择近乎一致(例如议会里的政党),足以改变选举结果。议会中政党会组成联盟以增加影响力。
改变现状
不少投票制度的要求比过半数更为严格,例如要求绝对多数才能改变现状,最极端的例子是要求全体一致通过的制度。如果投票旨在决定是否接受新成员加入,否决新成员加入的选票被称为“黑球反对票”(Blackball)。
另一种改变现状的机制,则要求参与投票人数符合法定最低人数要求。通常法定人数指参与投票人数,而不是投票支持的人数,但这种制度往往促使反对者以拒绝投票的方法,阻止会议达到法定人数。
选举区
选举通常为了选出多名立法机构成员。选举可以不划分选区,也可以由各自的选区选出代表。
 以色列以色列等国家便采用单一选区的制度来选出整个国会。而爱尔兰、比利时等则将国家划分为许多小型选区。美国、英国则采用单一获胜者的制度。一些则采用单一选区两票制,亦有将小型地区归入大型选区的制度。
以色列以色列等国家便采用单一选区的制度来选出整个国会。而爱尔兰、比利时等则将国家划分为许多小型选区。美国、英国则采用单一获胜者的制度。一些则采用单一选区两票制,亦有将小型地区归入大型选区的制度。
选区划分和议席分配的方式可能会戏剧性地改变选举结果。依据人口普查所得的人口数据,选区会重新分配议席数目。而重新划分选举区则是将选区的界线重新调整。两种过程都有可能改变选举的结果,因此都极具政治争议性。有时也可能被政治操作而导致选区划分不公,被称为杰利蝾螈(Gerrymandering)。
单一获胜者
单一获胜者的制度可以由选票的形式分类。二元投票制度里选民可以选择是否投给一个候选人。在次序投票制里选民依据其喜好排列候选人顺序。在计分投票制里,选民则替每个候选人打分数。
二元投票制
最普及的单一获胜者制度显然是多数制(也称为“最高票者当选制”、“相对多数决”、或“获胜者全得”)。每个选民投给一个选项,取得最多选票的选项获胜,即使没有取得半数亦然。
 在认可投票制里投票者可以自由投给任何选项认可投票制是另一种二元投票制的方法,选民可以投给每一个候选人,取得最多认可的候选人当选。
在认可投票制里投票者可以自由投给任何选项认可投票制是另一种二元投票制的方法,选民可以投给每一个候选人,取得最多认可的候选人当选。
与能投票制也是一种二元投票制的方法。选民在选票上可以圈选多个候选人(至于可圈选数,可依民情设定不同计算公式);而且选民必须在一张选票上恰好将圈项数全部用完,才算是有效票。
决赛投票制则以多回合的多数决选举来确保当选者是由多数选出。前两名决赛的投票是第二常用的选举方法,假如没有过半数的获胜者出现,便由得票数前两名的候选人再次进行决赛。在淘汰决赛选举里,名次最后的候选人会被逐一淘汰,直到出现过半数为止。而在消耗性决赛选举里,没有候选人会被淘汰,因此选举将不断重复直到出现过半数为止。
随机投票则是让每个投票者投给一个选项,并随机抽选一张选票来决定获胜者。这种方法大多是用于在其他方法产生平手结果时决赛之用。
排序投票制
也被称为优序投票制,这些方法让每个选民自行依照喜好排序候选人。通常并不一定需要排序所有的候选人:没有被排序的候选人通常会被计算为排序最低者。一些排序投票法也允许投票者将多重的候选人列为同一名次。
 典型的排序投票制里投票者依照喜好排列选项最常见的排序投票法是排序复选制(Instant-runoff voting, IRV),也被称为“顺位同票制”或“优序投票制”,投票者的排序能够扮演淘汰功能,而无须再进行额外的淘汰投票。在计算票数时,最少被列为第一顺位的选项将被淘汰。在接下来几轮的计票中,那些第一顺位已经被淘汰的选票所选择的第二顺位仍然有效。最少被选择的选项在一轮接着一轮的计票中被逐一淘汰,直到出现过半数的获胜者为止,过程中所有的选票在每一轮的计票中都会被计算到。
典型的排序投票制里投票者依照喜好排列选项最常见的排序投票法是排序复选制(Instant-runoff voting, IRV),也被称为“顺位同票制”或“优序投票制”,投票者的排序能够扮演淘汰功能,而无须再进行额外的淘汰投票。在计算票数时,最少被列为第一顺位的选项将被淘汰。在接下来几轮的计票中,那些第一顺位已经被淘汰的选票所选择的第二顺位仍然有效。最少被选择的选项在一轮接着一轮的计票中被逐一淘汰,直到出现过半数的获胜者为止,过程中所有的选票在每一轮的计票中都会被计算到。
波达计数法(Borda Count)是较为简单的排序投票法,每个选项借由选票上的排序来取得积分,积分最高者获胜。另一个类似的方法则是位置投票制。
孔多塞制
孔多塞制(Condorcet voting),或称双序制,是以孔多塞准则衍生的投票制度。这种方法将每个选项与所有其他的选项成对比较,一次一个,而击败所有其他选项的选项便是赢家。只要一个选项在大多数选票上的位置高于另一个选项,那么它便击败了那个选项。
这些方法通常被称为孔多塞制,因为孔多塞准则确保了它们在大多数选举中都能获得一样的结果,也就是存在着一个孔多塞赢家。不同孔多塞制之间的差别在于出现没有选项被击败时的情况,意味着产生了一个选项之间不断击败对方的循环,这被称为孔多塞悖论。为了解决孔多塞悖论的循环,当没有孔多塞赢家出现而选择特定孔多塞版本来决定赢家的状况被称为孔多塞完结法。
另一个简单的孔多塞制是最大最小(Minimax)制:如果没有选项没被击败,那么被最少的选票击败的选项获胜。近年来还有由马库斯·舒尔茨(Markus Schulze)设计的舒尔茨制,以及尼科劳斯·泰德曼(Nicolaus Tideman)设计的排列成双制(Ranked Pairs),两种方法都以达成众多投票制度评价标准为目标。
计分投票制
 在累积选举制里投票者自行分配票数给候选人计分制甚至比排序制更为灵活,但设计用来使用它们的方法并不多。每个投票者给每个选项评分,评分可以使用数字(例如从0至100)或者“等级”如A/B/C/D。
在累积选举制里投票者自行分配票数给候选人计分制甚至比排序制更为灵活,但设计用来使用它们的方法并不多。每个投票者给每个选项评分,评分可以使用数字(例如从0至100)或者“等级”如A/B/C/D。
在计分投票制里,投票者给予每个选项数字分数,总和分数最高的选项获胜。认可投票制或与能投票有时会使用0或1来表示认可与否,因此也可以被视为计分制的一种形式。
累积选举制则规定了一定的点数,由投票者自行配点。累积选举制也常被用于一些投票者权力不相等的投票中,例如依据股份采取“一张股票,一张选票”的公司投票。累积选举制也被用于多重获胜者的选举中,例如公司董事会成员的选举。
计分投票制也可以被用于排序投票制,只要排序制里允许选民排出同样名次的选项。一些排序制假定选票上的名次都不相同,但一些投票者也可能会给两个以上的候选项目相同的排名。
多重获胜者
会出现多重获胜者制度的选举,例如立法机构议员的选举,在实行上会与单一获胜者的选举不同。通常在多重获胜者选举中,参与者会较为关切己方在立法机构里取得的整体议席数量,而不是特定的候选人是否当选。也因此,许多多重获胜者选举都采用比例代表制,表示如果某个政党取得了X%的选票,那它们就能取得在立法机构里X%的议席数。但并非所有多重获胜者选举都会采用比例代表制。
非比例制和半比例制
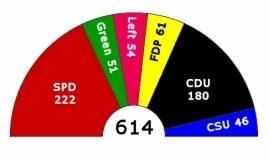 2005年德国联邦选举里每个政党赢得的议席许多多重获胜者选举都只简单地沿用单一获胜者选举的方法,而没有依照明确的比率。在集团投票制(Bloc voting)里,每个选区分配N个应选议席,得票数最高的前N名当选。由于时常会有一些压倒性的单一获胜者出现,因此集团投票并非比例制的。另外两种以多数决为基础的类似方式是复数选区单记不可让渡投票制和之前述及的累积选举制。与集团投票不同的是,在复数选区单记不可让渡投票制或累积选举制中,选民可能会采取配票或战略提名的方式而达成比例的平衡。
2005年德国联邦选举里每个政党赢得的议席许多多重获胜者选举都只简单地沿用单一获胜者选举的方法,而没有依照明确的比率。在集团投票制(Bloc voting)里,每个选区分配N个应选议席,得票数最高的前N名当选。由于时常会有一些压倒性的单一获胜者出现,因此集团投票并非比例制的。另外两种以多数决为基础的类似方式是复数选区单记不可让渡投票制和之前述及的累积选举制。与集团投票不同的是,在复数选区单记不可让渡投票制或累积选举制中,选民可能会采取配票或战略提名的方式而达成比例的平衡。
虽然这两种制度并没有保证比例的平衡,但选民的行动可能产生比例平衡的结果,也因此复数选区单记不可让渡投票制和累积选举制被分类为半比例制。其他可以被视为半比例制的方法还包括混合制—结合了普选与政党提名名单的选举。
比例制
真正的比例制则会以一些方式保证每个获胜的候选人都代表着相同数量的选票。这个数量被称为配额。举例而言,在一定的误差范围内,如果配额是1000张选票,那么每个当选的候选人就代表着1000张选票的民意。
大多数的比例制都是采用政党名单比例代表制,选民投给支持的政党而非特定的候选人,依据政党取得的选票配额数量分配议席。这些制度决定配额的方式也各有差异,相同的,在如何搭配选票数量和议席数量上的方式也有差异。
分配议席的方式可以被分类为最高平均数法和最大余额方法。最大余额法以选票的数量设定特定的配额,而最高平均数法则直接除以选票的数量来决定配额。
政党的名单可以分为开放名单或是封闭名单,在开放名单制度里,投票者能决定要投给政党里的哪个特定候选人。在封闭名单制度里,议席则由政党自行分派。而混合比例制度(Mixed Member Proportional, MMP)则结合了两种名单的方法,只以政党的名单作为辅助,搭配地区性选举所选出的议席,因此有了两种名单制度的特色。
与政党名单制度相较,单记可让渡投票制则是由选民依照喜好排列候选人的比例代表制。与政党名单不同的是,单记可让渡投票制并非取决于候选人的政党,选票是经由和排序复选制类似的方法转移,计票时选票上的所有排序都会被计算到。
投票制度标准
在现实世界,人们对于一个投票制度的态度往往取决于那个制度对他们支持或反对的政党所产生的影响。这使得要客观评估一个投票制度变的相当困难。为了能够公正而不带意识形态的比较投票制度,投票理论家使用投票制度标准,在数学上定义投票制度的理想属性。
 肯尼斯·约瑟夫·阿罗一个投票制度是不可能达成所有标准的。经济学家肯尼斯·约瑟夫·阿罗提出了阿罗不可能定理(Arrow's impossibility theorem),指出几种投票制度各自的优点是互相矛盾的,也因此,选择投票制度时必须衡量到哪种标准才适用于那次选举。
肯尼斯·约瑟夫·阿罗一个投票制度是不可能达成所有标准的。经济学家肯尼斯·约瑟夫·阿罗提出了阿罗不可能定理(Arrow's impossibility theorem),指出几种投票制度各自的优点是互相矛盾的,也因此,选择投票制度时必须衡量到哪种标准才适用于那次选举。
使用这些标准来衡量投票制度并不一定是完全客观的。举例而言,要设计一个和某种投票制度符合的标准并不困难,但这种带有偏见的评量标准却没有考虑到其他方法的存在。没有人能确定何种标准才是正确的,以下只是一些被多数投票理论家认同的标准:
1.多数决标准 — 如果有一个被多数人所支持的候选人存在,他是不是一定能获胜呢?
2.单调性标准 — 在选票转移的过程中,一个原本获得更高顺序的候选人是否会因此失败,而一个原本顺序较低的候选人是否会因此当选?(举例而言,有三个候选人甲乙丙,甲获得最多选民列为第一支持对象,乙次之,丙则获得最少,因此丙被淘汰。但紧接着丙的选票被转移,之中将乙列为第二支持对象的较多,进而逆转原先第一支持对象的结果,使甲落选)
3.一致性标准 — 如果将全体选票切割为两半各自计票,得出的结果是否与原先一致?
4.参与度标准 — 投票制度是否会导致故意不参与投票的现象出现?(举例而言,在法定最低人数的限制下,投票者可能会采取拒绝投票的方式)
5.孔多塞标准 — 如果一个候选人在个别的成对比较里击败了所有候选人,他是不是一定能获胜呢?
6.孔多塞输家标准 — 如果一个候选人在个别的成对比较里输给了所有候选人,他是不是一定会输掉呢? 7.独立性标准 — 如果添加或移除失败的候选人的选票,结果是否一定相同?
8.无复制标准 — 如果添加与候选人完全相同的克隆人参与,结果是否会相同? 以下列表显示了这些标准对一些单一获胜者制度的评价,排列顺序大致等同它们在现实世界的普及性。
| 多数决 | 单调性 | 一致性 | 参与度 | 孔多塞 | 孔多塞输家 | 独立性 | 无复制 | |
| 多数制 | 是 | 是 | 是 | 是 | 否 | 否 | 否 | 否 (票源分割) |
| 复选制 | 是 | 否 | 否 | 否 | 否 | 是 | 否 | 否 (票源分割) |
| 排序复选制 | 是 | 否 | 否 | 否 | 否 | 是 | 否 | 否 (票源分割) |
| 认可制 | 否 | 是 | 是 | 是 | 否 | 否 | 是 | 不一定 |
| 与能投票制 | 否 | 是 | 是 | 是 | 否 | 否 | 是 | 不一定 |
| 计分投票制 | 否 | 是 | 是 | 是 | 否 | 否 | 是 | 不一定 |
| 波达计数法 | 否 | 是 | 是 | 是 | 否 | 是 | 否 | 否 (战略提名) |
| 最大最小 | 是 | 是 | 否 | 否 | 是 | 否 | 否 | 否 (票源分割) |
| 舒尔茨制 | 是 | 是 | 否 | 否 | 是 | 是 | 否 | 是 |
| 排列成双 | 是 | 是 | 否 | 否 | 是 | 是 | 否 | 是 |
除了以上的标准以外,仍有一些无法以数学衡量的投票制度标准,例如制度的简易性、计票速度、过程中被操弄或结果引发争议的可能性、造成战术投票和战略提名现象的可能性,以及在多重获胜者制度中分配比例的平均性,这些也都是相当重要的。
投票理论创立
| 多数决 | 单调性 | 一致性 | 参与度 | 孔多塞 | 孔多塞输家 | 独立性 | 无复制 | |
| 多数制 | 是 | 是 | 是 | 是 | 否 | 否 | 否 | 否 (票源分割) |
| 复选制 | 是 | 否 | 否 | 否 | 否 | 是 | 否 | 否 (票源分割) |
| 排序复选制 | 是 | 否 | 否 | 否 | 否 | 是 | 否 | 否 (票源分割) |
| 认可制 | 否 | 是 | 是 | 是 | 否 | 否 | 是 | 不一定 |
| 与能投票制 | 否 | 是 | 是 | 是 | 否 | 否 | 是 | 不一定 |
| 计分投票制 | 否 | 是 | 是 | 是 | 否 | 否 | 是 | 不一定 |
| 波达计数法 | 否 | 是 | 是 | 是 | 否 | 是 | 否 | 否 (战略提名) |
| 最大最小 | 是 | 是 | 否 | 否 | 是 | 否 | 否 | 否 (票源分割) |
| 舒尔茨制 | 是 | 是 | 否 | 否 | 是 | 是 | 否 | 是 |
| 排列成双 | 是 | 是 | 否 | 否 | 是 | 是 | 否 | 是 |
单一获胜者制
 让-查理斯·波达是早期的投票理论家投票理论在法国大革命时期浮现成为学术界的一门研究领域。让-查理斯·波达(Jean-CharlesdeBorda)在1770年提出了波达计数法来选举法国科学院(Académiedessciences)的成员。他的制度被马奎斯·孔多塞(MarquisdeCondorcet)所反对,孔多塞另外发明了一种成双比对法。孔多塞的方法成为了孔多塞制。
让-查理斯·波达是早期的投票理论家投票理论在法国大革命时期浮现成为学术界的一门研究领域。让-查理斯·波达(Jean-CharlesdeBorda)在1770年提出了波达计数法来选举法国科学院(Académiedessciences)的成员。他的制度被马奎斯·孔多塞(MarquisdeCondorcet)所反对,孔多塞另外发明了一种成双比对法。孔多塞的方法成为了孔多塞制。
波达和孔多塞通常被视为投票理论的创始人,不过最近的研究则显示哲学家雷蒙·卢尔(RamonLlull)早在13世纪便以发现波达计数法和孔多塞标准,记载了这些发现的手稿一直到2001年才被发现。
在18世纪后期,与选区划分有关的议题也开始被研究。由于美国宪法规定众议院必须依照各州的人口分配议席,但却没有指定如何分配,因此开始了针对如何公平划分选区的研究。亚历山大·汉弥尔顿(AlexanderHamilton)、托马斯·杰斐逊、和丹尼尔·韦伯斯特(DanielWebster)等政治家都提出了各种解决方案。一些美国的分配方式后来也在19世纪的欧洲运用,用以在新的政党名单比例代表制里划分议席。
单记可让渡投票制在1855年由丹麦数学家卡尔·安德烈(CarlAndræ)发明,英国的索玛斯·黑尔(ThomasHare)也在1857年发明了这种制度。1856年的丹麦选举和1896年的塔斯马尼亚都采用了单记可让渡投票制。政党名单比例代表制在20世纪初期于欧洲出现,用以选举立法机构议员,第一个采用的是1900年的比利时。从那时开始,几乎每个民主国家都采用了比例制或半比例制的方法,除了英国的前殖民地例外。
对博弈论影响
或许是受到多重获胜者制投票方法的快速发展所影响,19世纪时理论家们也开始发表关于单一获胜者制的新方法。这开始于1870年左右,WilliamRobertWare提议将单记可让渡投票制的方法运用至单一获胜者制的选举,产生了排序复选制[6]很快地,数学家们开始重新捡视孔多塞的概念,并发明了新的方法以达成孔多塞完结。EdwardJ.Nanson结合了新的排序复选制与波达计算法,创造出一种新的孔多塞方法。路易斯·卡罗发行了关于投票理论的小册子,专门针对孔多塞的制度,他提出以矩阵来分析孔多塞选举的方法,不过这些方法也是早在13世纪雷蒙·卢尔的手稿里便已被提出。他也提出了一种直接的孔多塞方法,被称为卡罗制。
排序投票制也取得了更多支持而得以运用在政府选举里。在澳大利亚,排序复选制首先在1893年被采用,并一直维持。在20世纪初期,美国的许多市镇开始采用巴克林投票制(Bucklinvoting),但选民对产生的结果不满,不久后巴克林投票制便不再采用,并且在明尼苏达州被宣布违反了宪法。
发展现状
自从约翰·冯·诺伊曼和其他人在1940年代将博弈论带进数学领域后,有了新的数学工具能用以分析投票制度和投票的策略。这使得投票理论的领域产生重要的改变。肯尼斯·约瑟夫·阿罗提出了阿罗不可能定理,证明在投票制度的评价里,有些标准其实是互相矛盾的,也证明了投票定理的固有限制。阿罗的定理是早期投票理论最常引用的,也产生了进一步的重要理论,例如吉伯-萨特维定理(Gibbard-Satterthwaitetheorem),显示在许多一般情况下,战略投票是不可避免的现象。
运用博弈论来分析投票制度也使人们发现了一些投票制度里所带来意外影响。杜伟杰法则(Duverger'slaw)便是这种例子之一,显示了多数制经常会产生两党制的结果。

-
汽车维修维修竣工出厂合格证制度
2025-11-03 04:06:00 查看详情 -
修理厂维修管理制度(4S店业务管理制度——维修车间安全操作规程汇编)
2025-11-03 04:06:00 查看详情 -
保险中介相关法规制度汇编
2025-11-03 04:06:00 查看详情 -
汽车安全 汽车的安全管理制度和安全保护措施是什么?
2025-11-03 04:06:00 查看详情 -
缺陷汽车产品召回管理条例 汽车召回是在哪里修召回制度
2025-11-03 04:06:00 查看详情 -
汽车召回制度 汽车召回有补偿吗
2025-11-03 04:06:00 查看详情


 求购
求购



