- 基波分量

基波分量
周期信号分析
一个周期信号可以通过傅里叶变换分解为直流分量c0和不同频率的正弦信号的线性叠加:
其中,cm表示m次谐波的幅值,其角频率为mω,初始相位为φm,其有效值为cm/√2。
当m=1时,为基波分量的表达式,其角频率为ω,初始相位为φ1,其方均根值c1/√2称为基波有效值。
ω/2π为基波分量的频率,称为基波频率,基波分量的频率等于交流信号的频率。而m次谐波的频率为基波频率的整数倍(m倍)。
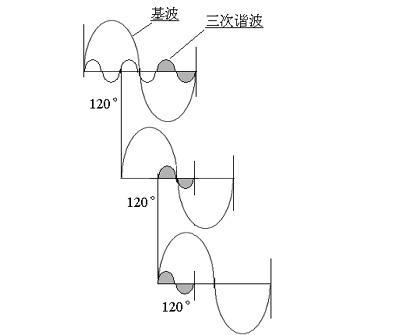
测量方法
当信号的谐波频率与基波频率差距较大时,即信号的基次谐波含量较小,主要为基波时,可以通过低通滤波的方法将高次谐波滤除,剩下就是信号的基波,采用均值检波表、峰值检波表和真有效值检波表均可测量其有效值,测量结果近似等于基波有效值。
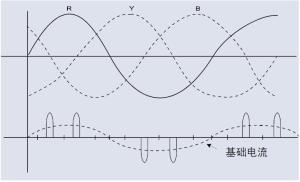 当信号频谱较复杂时,尤其是次谐波含量较大时,很难用滤波的方法将基波准确分离,一般先用交流采样获取离散时间信号序列,再用离散傅里叶变换(DFT或FFT)对其进行傅里叶展开,即可求得基波有效值。各种谐波分析仪和宽频功率分析仪(变频功率分析仪、高精度功率分析仪等)等设备均可测量适用频率范围内交流信号的基波有效值。上述仪器除了测量电压、电流的基波有效值之外,还具备功率测量及谐波测量功能。
当信号频谱较复杂时,尤其是次谐波含量较大时,很难用滤波的方法将基波准确分离,一般先用交流采样获取离散时间信号序列,再用离散傅里叶变换(DFT或FFT)对其进行傅里叶展开,即可求得基波有效值。各种谐波分析仪和宽频功率分析仪(变频功率分析仪、高精度功率分析仪等)等设备均可测量适用频率范围内交流信号的基波有效值。上述仪器除了测量电压、电流的基波有效值之外,还具备功率测量及谐波测量功能。
提取及应用
提取方法及在有源滤波器中的应用
在电能质量调节装置中,基波分量的提取精度和速度在很大程度上影响其性能。根据最小二乘原理,提出一种提取基波分量的方法。方法精度高,跟踪性能好,对基波突变甚至频率波动有较快的响应时间和较好的跟踪性能。由该方法得到的基波相角可以作为系统的同步信号。对信号处理算法进行了数学推导和实验研究,并将该方法应用于[1]有源滤波器实验装置中,实验结果验证了其有效性。

相关百科
-
上汽大众汽车有限公司宁波分公司
2025-09-22 05:46:08 查看详情


 求购
求购







