- Sobolev空间

Sobolev空间
简介
对于数学函数的光滑性有很多种。最基本的要求可能就是函数要连续,更进一步的要求是导数(因为可微函数也是连续的),再强一些的概念是导数的连续性(这些函数称为![]() — 参看光滑函数)。可微函数在很多领域相当重要,特别是在微分方程中。在二十世纪,人们发现
— 参看光滑函数)。可微函数在很多领域相当重要,特别是在微分方程中。在二十世纪,人们发现![]() 函数空间不是研究微分方程的解的恰当的空间。
函数空间不是研究微分方程的解的恰当的空间。
而索博列夫空间正是![]() 空间的替代品,用于研究偏微分方程的解。
空间的替代品,用于研究偏微分方程的解。
技术性讨论
我们从最简单情况下的索博列夫空间开始,也就是单位圆上的一维情况。在这个情况下,索博列夫空间![]() 定义为L的子集,使得f和它的直到k阶的导数有一个有限的L范数,对于某个给定的p≥ 1。定义正确意义上的导数时必须小心。在这个一维问题中,假设
定义为L的子集,使得f和它的直到k阶的导数有一个有限的L范数,对于某个给定的p≥ 1。定义正确意义上的导数时必须小心。在这个一维问题中,假设![]() 是几乎处处可微并且等于其导数的勒贝格积分(这可以排除康托函数这样的例子)就足够了。
是几乎处处可微并且等于其导数的勒贝格积分(这可以排除康托函数这样的例子)就足够了。
按照这个定义,索博列夫空间有一个自然的范数,
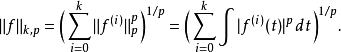
赋予了范数![]() 的
的![]() 是一个完备空间。实际上只要取序列中的第一项和最后一项就可以了,也即,如下的范数
是一个完备空间。实际上只要取序列中的第一项和最后一项就可以了,也即,如下的范数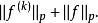 和上述范数等价。
和上述范数等价。
例子
有些索博列夫空间有简单的表述。例如,在一维情况,![]() 就是绝对连续函数空间,而W是李普希兹函数空间。还有,
就是绝对连续函数空间,而W是李普希兹函数空间。还有,![]() 可以自然地用其傅立叶级数的术语定义,也就是
可以自然地用其傅立叶级数的术语定义,也就是
![]() 其中
其中![]() 是f的傅立叶级数。和前面一样,可以采用等价的范数
是f的傅立叶级数。和前面一样,可以采用等价的范数
![]() 两个表达都可以从帕塞瓦尔定理以及微分等价于傅立叶系数乘以in这个事实导出。
两个表达都可以从帕塞瓦尔定理以及微分等价于傅立叶系数乘以in这个事实导出。
非整数k情况
为避免混淆,在讨论不是整数的k的时候,我们通常用s来取代它,也即![]() 或者
或者![]() 。
。
p等于2
p= 2的情形是最简单的情形,因为傅立叶表述可以直接推广。我们定义范数为
![]()
而索博列夫空间![]() 为具有有限范数的函数的空间。
为具有有限范数的函数的空间。
分数阶微分
如果p不是2,就采取类似的方法。在这个情况下帕塞瓦尔定理不再成立,但是微分还是对应于在傅立叶域中的乘法,并且可以推广到非整数阶。因此,可以定义一个分数阶微分的算子其阶为s,如下所示
![]()
换句话说,取傅立叶变换,乘以![]() 再取逆傅立叶变换(定义为傅立叶-乘法-逆傅立叶的算子称为乘子,这本身也是一个研究主题)。这使得我们可以定义
再取逆傅立叶变换(定义为傅立叶-乘法-逆傅立叶的算子称为乘子,这本身也是一个研究主题)。这使得我们可以定义![]() 的索博列夫范数如下
的索博列夫范数如下
![]() 而且,跟平常一样,索博列夫空间是有有限索博列夫范数的函数的空间。
而且,跟平常一样,索博列夫空间是有有限索博列夫范数的函数的空间。
复插值
获取“分数索博列夫空间”的另一个办法是采用复插值。复插值是一个通用的技术:对于任何0 ≤ t ≤ 1 和巴拿赫空间X及Y,且这二者都包含于某个更大的巴拿赫空间中,我们可以创建“过渡空间”,记为[X,Y]t。(后面将会讨论到一个不同的方法,所谓的实插值方法,它对于迹的分类的索博列夫理论有重要的意义)。
多维情况
现在考虑在R及其子集上的索博列夫空间。从圆到线的变化只涉及傅立叶公式的技术细节 — 基本上就是将傅立叶级数变为傅立叶变换,将求和变为积分。到多维情况的转换有更大的难度,从定义就开始变化。![]() 是
是![]() 的积分这个条件无法一般化,而最简单的解决办法是考虑分布理论意义下的导数。
的积分这个条件无法一般化,而最简单的解决办法是考虑分布理论意义下的导数。
由此可以得到一个形式化的定义。令D为R中开集。定义索博列夫空间
![]()
![]() 为定义于D上的函数f的族,使得对于满足下式的每个多重索引
为定义于D上的函数f的族,使得对于满足下式的每个多重索引
![]()
![]() 是一个函数,且
是一个函数,且
![]()
在它上面的一个合适的范数是所有这样的α上的那些L范数的和。它是完备的,因此是一个巴拿赫空间。
实际上,这个方法在一维也成立,并且和前面分数阶微分中所述并无多大区别。
在多维情况,有些结果不再成立,例如,![]() 只包含连续函数。例如,1/|x|属于
只包含连续函数。例如,1/|x|属于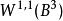 ,其中
,其中![]() 是三维的单位球。对于足够大的k,
是三维的单位球。对于足够大的k,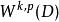 将只包含连续函数,但是对于哪个k才够取决于p以及维数这二者。
将只包含连续函数,但是对于哪个k才够取决于p以及维数这二者。
但是,W和![]() 的表述在做了必要的修改之后还是成立的。
的表述在做了必要的修改之后还是成立的。
索博列夫嵌入
索博列夫空间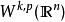 是
是![]() 的子集。一个很自然的问题是:有没有其它的L空间包含
的子集。一个很自然的问题是:有没有其它的L空间包含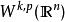 ?索博列夫嵌入定理给出一个简单的表达(参看):
?索博列夫嵌入定理给出一个简单的表达(参看):
定理:令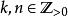 且
且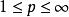 。则如下命题成立:
。则如下命题成立:
若![]() 则
则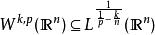 (作为集合)。而且,包含关系是一个有界算子。
(作为集合)。而且,包含关系是一个有界算子。
若![]() 则所有有紧支撑的函数
则所有有紧支撑的函数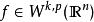 是
是![]() 的元素,其中
的元素,其中![]() 。
。

-
PRO上市 售价9.48万
2025-08-23 14:10:28 查看详情 -
江铃福特轻客持续打造最优TCO 锐骐超值版PK江铃国产共轨
2025-08-23 14:10:28 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-08-23 14:10:28 查看详情 -
Plus上市 别克昂科威S及昂科威S艾维亚将于7月29日上市
2025-08-23 14:10:28 查看详情 -
全新紧凑型SUV/上半年上市 别克昂科拉PLUS最新谍照
2025-08-23 14:10:28 查看详情 -
黄海纯电轿车Smile将于12月上市 29万元
2025-08-23 14:10:28 查看详情 -
江铃宝典堪称商用皮卡常青树 江铃新宝典VS长城风骏7(图文)
2025-08-23 14:10:28 查看详情 -
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-08-23 14:10:28 查看详情 -
实拍江铃新宝典(图文) 空间满足家用
2025-08-23 14:10:28 查看详情 -
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-08-23 14:10:28 查看详情


 求购
求购

