- 渐近正态估计

渐近正态估计
基本介绍
相合性反映了当![]() 时估计量的优良性质,但由于参数
时估计量的优良性质,但由于参数![]() 的相合估计可以不止一个,它们之间的差异可以用估计量的渐近分布的渐近方差反映出来。
的相合估计可以不止一个,它们之间的差异可以用估计量的渐近分布的渐近方差反映出来。
定义设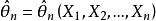 是
是![]() 的估计量,如果存在一串
的估计量,如果存在一串![]() ,满足
,满足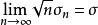 ,其中
,其中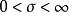 ,使得当
,使得当![]() 时,有
时,有
![]() 的分布收敛于N(0,1)
的分布收敛于N(0,1)
则称![]() 是
是![]() 的渐近正态估计,
的渐近正态估计,![]() 称为
称为![]() 的渐近方差。
的渐近方差。
当样本容量n足够大时,对于一个渐近正态估计![]() ,可以用
,可以用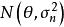 作为
作为![]() 的近似分布,从而可以对
的近似分布,从而可以对![]() 进行区间估计。
进行区间估计。
容易证明,渐近正态估计一定是相合估计,但不一定是强相合估计。
对某个待估参数![]() ,如果存在着渐近正态估计,这样的估计可能并不唯一。因此渐近方差的大小就可以作为比较这些估计优劣的一个准则。
,如果存在着渐近正态估计,这样的估计可能并不唯一。因此渐近方差的大小就可以作为比较这些估计优劣的一个准则。
相关概念与定理
最优渐近正态估计设![]() 为待估参数
为待估参数![]() 的一个渐近正态估计,渐近方差为
的一个渐近正态估计,渐近方差为![]() ,若对
,若对![]() 的任意渐近正态估计
的任意渐近正态估计![]() ,渐近方差记内
,渐近方差记内![]() 、有
、有
![]() 则称
则称![]() 为
为![]() 的最优渐近正态估计(the best asymptotically normal estimate)[1]。
的最优渐近正态估计(the best asymptotically normal estimate)[1]。
定理渐近正态估计一定是相合估计。
证明: 设![]() 是
是![]() 的渐近正态估计,由定义,对任意
的渐近正态估计,由定义,对任意![]() 及k>0,当n充分大时
及k>0,当n充分大时![]() 必须充分小,因此
必须充分小,因此![]() ,故当
,故当![]() 时有
时有
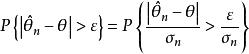
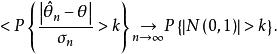 由k的任意性,令
由k的任意性,令![]() ,由于
,由于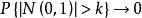 ,因此
,因此
![]() 即
即![]() 是
是![]() 的相合估计[2]。
的相合估计[2]。
例题解析
例1设X~B(1,p)(二项分布),(X1,X2,…,Xn)是X的样本,p的一个估计量是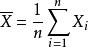 ,由中心极限定理,当
,由中心极限定理,当![]() 时有
时有
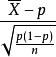 的渐近分布为N(0,1),
的渐近分布为N(0,1),
故![]() 是p的渐近正态估计,渐近方差为
是p的渐近正态估计,渐近方差为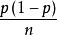 。
。

相关百科
-
上海正艺信息科技有限公司
2025-09-25 05:51:48 查看详情


 求购
求购






