外接球

在中学的立体几何中，有关多边形内切球和多边形外接球半径的计算题目，占有重要的地位，现在来简述一下这些球的基本性质。

多边形内切球球心是多边形一切二面角平分面的交点。

多边形外接球球心O的位置可用下述方法之一定出来：

1)点O是通过多面体非平行平面外接圆的圆心并垂直于非平行平面的两条直线的交点；

2)点O是通过多面体非平行棱中点、并垂直于这些棱的三个平面的交点；

3)点O是通过一个面的外接圆圆心，且垂直于此圆的平面∑的直线和垂直于过不与∑平行的棱的中点的平面，且垂直于此棱的直线的交点。

一个球面是由四个非共面的点所确定的。因此，求解多面体外接球半径的任何习题都可由其内切球的证明和计算绕某个三棱柱外接球的半径(顶点是给定多面体的顶点)得出来^[1]。

长方体一定有外接球，外接球的球心即其体对角线的交点，半径为体对角线的一半。

正方体既有内切球，也有外接球，球心都是体对角线的交点，内切球的半径为棱长的一半，外接球的半径为体对角线的一半。

长方体外接球的直径=长方体的体对角线长。

正方体外接球的直径=正方体的体对角线长。

圆柱体外接球的直径=圆柱体的体对角线长^[1]。

正方体的外接球半径与内接球半径之比为。

【例1】 已知正方体外接球的体积是，那么正方体的棱长等于(  )。

A.B.C.D.

【分析】正方体外接球的直径为体对角线。

【解析】设正方体的棱长为a，外接球半径为R，则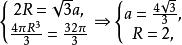故选D。

【例2】若圆柱体的高增大到原来的2倍，底面积增大到原来的4倍，则其外接球的体

积增大到原来的外接球的体积的倍数是(  )．

A．4.5         B．8            C．9               D．16             E．-15

【解析】 设原来的圆柱体的底面半径为r，高为h，外接球的半径为，

则

现在的圆柱体的底面半径为2r，高为2h，外接球的半径为，则

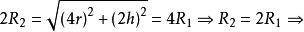体积倍数为8。

综上所述，答案是B。