- 等度连续

等度连续
定义
命![]() (或写成
(或写成![]() )为定义在实数集E上一列实数值函数,我们说
)为定义在实数集E上一列实数值函数,我们说![]() 在E上是等度连续的,倘若对任意
在E上是等度连续的,倘若对任意![]() 存在一个
存在一个![]() ,使得凡当
,使得凡当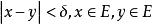 及
及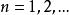 的时候都有[1]
的时候都有[1]

相关命题
命题1
命K为一个实数的紧致集,若![]() 在K上是一个一致收敛的连续函数的序列,则
在K上是一个一致收敛的连续函数的序列,则![]() 在K上是等度连续的。
在K上是等度连续的。
证明:设给定![]() ,则存在一整数n0及
,则存在一整数n0及![]() 使得,对一切
使得,对一切![]() 及
及![]()
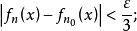 因为在紧致集上连续的函数是一致连续的,我们有
因为在紧致集上连续的函数是一致连续的,我们有
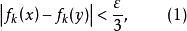 对
对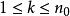 及
及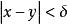 成立,因此,若
成立,因此,若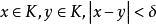 与
与![]() 我们有
我们有
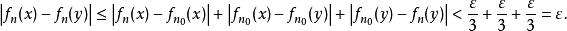 这与(1)一起证明了命题。[2]
这与(1)一起证明了命题。[2]
定义1
命![]() 为定义在实数集E上的一个实数值函数序列,我们说
为定义在实数集E上的一个实数值函数序列,我们说![]() 在E上是点式有界,倘若序列
在E上是点式有界,倘若序列![]() 对每一
对每一![]() 有界,就是说,倘若存在一个有限值函数h,定义在E上,使得
有界,就是说,倘若存在一个有限值函数h,定义在E上,使得
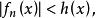 对一切
对一切![]() 及一切
及一切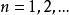 成立。
成立。
我们回忆一下![]() 在E上叫做一致有界,倘若有一实数M使得
在E上叫做一致有界,倘若有一实数M使得
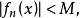 对一切
对一切![]() 及
及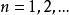 成立。
成立。
命题2
命K为一实数紧致集,如果![]() 在K上是点式有界及等度连续,则
在K上是点式有界及等度连续,则![]() 在K上一致有界。
在K上一致有界。
证明:我们定义
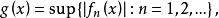 给定
给定![]() 我们选取
我们选取![]() 使得
使得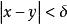 蕴涵
蕴涵
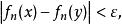 对n=1,2,…成立,如果我们固定两点x与y,不等式
对n=1,2,…成立,如果我们固定两点x与y,不等式
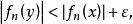 蕴涵
蕴涵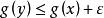 以及不等式
以及不等式
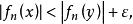 蕴涵
蕴涵 ;因此凡当
;因此凡当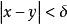 的时候,
的时候,
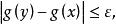 故
故![]() 在K上是连续的,因为K是紧致的,故
在K上是连续的,因为K是紧致的,故![]() 为有界。[2]
为有界。[2]
命题3
(阿斯科利-阿尔采拉(Ascoli-Arzela)定理)命K为实数的一紧致集,若![]() 在K上是点式有界及等度连续,则
在K上是点式有界及等度连续,则![]() 在集K上含有一个一致收敛的子序列。
在集K上含有一个一致收敛的子序列。
证明:命E为K的一切有理点的集,则E是可数的,并且K是E的闭包,命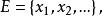 则
则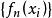 是一有界序列,由Bolzano-Weierstrass定理,可选取
是一有界序列,由Bolzano-Weierstrass定理,可选取![]() 的一个子序列
的一个子序列![]() 使得
使得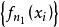 收敛,不妨设
收敛,不妨设
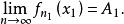 再考虑
再考虑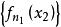 ,由Bolzano-Weierstrass定理,可以选取
,由Bolzano-Weierstrass定理,可以选取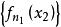 的一个子序列
的一个子序列![]() 使得
使得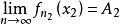 存在。
存在。
继续这样下去,得到一个子序列![]() 对m=1,2,…,使得
对m=1,2,…,使得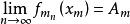 存在,m=1,2,….然后考虑对角线序列
存在,m=1,2,….然后考虑对角线序列![]() 。
。
对固定的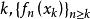 是
是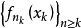 的一个子序列,因此收敛于
的一个子序列,因此收敛于![]() ,所以
,所以![]() 在E的每一点上收敛。
在E的每一点上收敛。
对任意![]() ,由于
,由于![]() 在K上等度连续,存在一个
在K上等度连续,存在一个![]() ,使得
,使得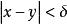 以及n≥1,有
以及n≥1,有
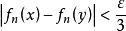
因为K为E的闭包,且是紧致集,在E内有有限多个点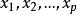 ,使得
,使得
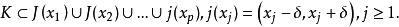 选取n0,使得
选取n0,使得
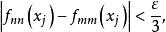 对
对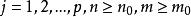 都成立。
都成立。
于是,对任意的![]() ,有一点
,有一点![]() ,其中
,其中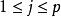 ,使得
,使得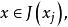 当
当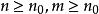 时,有
时,有
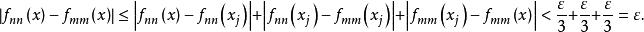 因此,
因此,![]() 在K上一致收敛。[1]
在K上一致收敛。[1]
 收藏
收藏

-
长城炮打造全场景皮卡车生活 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情 -
长城炮乘用皮卡全球版 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情 -
长城造 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情 -
长城炮带你开启浪漫之旅 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情 -
听听长城风骏车主怎么说 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情 -
长城炮带来野奢体验 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情 -
长城炮带你清凉一夏 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情 -
长城炮开启休旅新玩法 连续23年销冠是怎样炼成的
2025-09-16 05:25:26 查看详情


 求购
求购

