- 残差图

残差图
定义
以残差![]() 为纵坐标,以拟合值
为纵坐标,以拟合值![]() 或对应的数据观测序号
或对应的数据观测序号![]() 或数据观测时间为横坐标的散点图统称为残差图。残差图是进行模型诊断的重要工具。[2]
或数据观测时间为横坐标的散点图统称为残差图。残差图是进行模型诊断的重要工具。[2]
回归值与残差的残差图
为检验建立的多元线性回归模型是否合适,可以通过回归值![]() 与残差的散点图来检验。其方法是画出回归值
与残差的散点图来检验。其方法是画出回归值![]() 与普通残差的散点图
与普通残差的散点图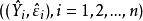 ,或者画出回归值
,或者画出回归值![]() 与标准残差的散点图
与标准残差的散点图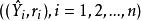 ,其图形可能会出现下面三种情况(如图1所示):
,其图形可能会出现下面三种情况(如图1所示):
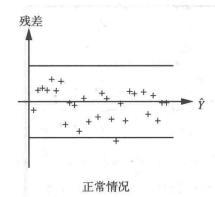 图1(a)
图1(a)
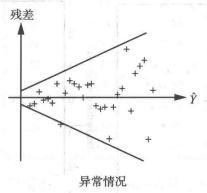 图1(b)
图1(b)
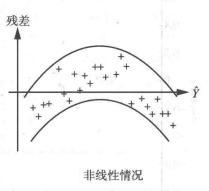 图1(c)
图1(c)
对于图1(a)的情况,不论回归值![]() 的大小,而残差
的大小,而残差![]() (或
(或![]() )具有相同的分布,并满足模型的各假设条件;对于图1(b)的情况,表示回归值
)具有相同的分布,并满足模型的各假设条件;对于图1(b)的情况,表示回归值![]() 的大小与残差的波动大小有关系,即等方差性的假设有问题;对于图1(c),表示线性模型不合适的样本,可能有异常值存在。
的大小与残差的波动大小有关系,即等方差性的假设有问题;对于图1(c),表示线性模型不合适的样本,可能有异常值存在。
对于图1(a),如果大部分点都落在中间(b)部分,而只有少数几个点落在外边,则这些点对应的样本,可能有异常值存在。[2]
以自变量为横坐标的残差图
以每个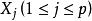 的各个观测值
的各个观测值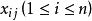 为点的横坐标,即以自变量为横坐标的残差图。与拟合值
为点的横坐标,即以自变量为横坐标的残差图。与拟合值![]() 为横坐标的残差图一样,满意的残差图呈现图1(a)的水平带状。如果图形呈现图1(b)的形状,则说明误差是等方差的假设不合适。若呈现图1(c)的形状,则需要在模型中添加
为横坐标的残差图一样,满意的残差图呈现图1(a)的水平带状。如果图形呈现图1(b)的形状,则说明误差是等方差的假设不合适。若呈现图1(c)的形状,则需要在模型中添加![]() 的高次项,或者对
的高次项,或者对![]() 作变换。
作变换。
残差的QQ图
设![]() 是残差
是残差![]() 的次序统计量,
的次序统计量, ,令
,令
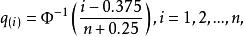 其中,
其中,![]() 为标准正态分布
为标准正态分布 的分布函数,
的分布函数,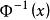 为反函数。称
为反函数。称![]() 为
为![]() 的期望值。
的期望值。
可以证明,若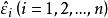 是来自正态分布总体的样本,则点
是来自正态分布总体的样本,则点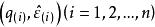 应在一条直线上。因此,若残差的正态QQ图中的点的大致趋势明显地不在一条直线上,则有理由怀疑对误差的正态性假设的合理性;否则可认为误差的正态性假设是合理的。[2]
应在一条直线上。因此,若残差的正态QQ图中的点的大致趋势明显地不在一条直线上,则有理由怀疑对误差的正态性假设的合理性;否则可认为误差的正态性假设是合理的。[2]
残差个案排序图
在MATLAB中,还可以通过rcoplot()函数画出残差个案排序图形,以此来判断样本是否为异常值样本,其使用格式为:rcoplot(r,rint)。
其中,参数r为回归残差,rint为残差的预测区间。[2]
 收藏
收藏

-
最新官图发布/将于年内上市 承载式车身结构/年内正式上市
2025-11-01 05:25:41 查看详情 -
Edition上市 全新奔腾B70官图曝光
2025-11-01 05:25:41 查看详情 -
黄海纯电轿车Smile将于12月上市 极氪009实车图曝光
2025-11-01 05:25:41 查看详情 -
路特斯ELETRE将于今日上市 蔚来EC6申报图曝光
2025-11-01 05:25:41 查看详情 -
江南U2正式上市 新款东风风行菱智M5官图发布
2025-11-01 05:25:41 查看详情 -
长安凯程GDI双侠成都上市 新款星途揽月官图
2025-11-01 05:25:41 查看详情 -
款帝豪GL将于3月25日正式上市 2023款奇瑞小蚂蚁官图
2025-11-01 05:25:41 查看详情 -
小鹏全新P7i将于今日上市 2023款奇瑞小蚂蚁官图
2025-11-01 05:25:41 查看详情 -
计划第三季度上市 2023款奇瑞小蚂蚁官图
2025-11-01 05:25:41 查看详情 -
风光SUV首付真0元 名图纯电动轻松拥有
2025-11-01 05:25:41 查看详情


 求购
求购
