- 正棱柱

正棱柱
棱柱
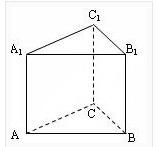 图1.正三棱柱棱柱是几何学中的一种常见的三维多面体,指两个平行的平面被三个或以上的平面所垂直截得的封闭几何体。
图1.正三棱柱棱柱是几何学中的一种常见的三维多面体,指两个平行的平面被三个或以上的平面所垂直截得的封闭几何体。
若用于截平行平面的平面数为n,那么该棱柱便称为n-棱柱。如三棱柱就是由两个平行的平面被三个平面所垂直截得的封闭几何体。[1]
棱柱的各种属性
底面
棱柱中两个互相平行的面,叫做棱柱的底面与侧面垂直。
侧面
棱柱中除两个底面以外的其余各个面都叫做棱柱的侧面。
侧棱
棱柱中两个侧面的公共边叫做棱柱侧棱。
顶点
棱柱中侧面与底面的公共顶点叫做棱柱的顶点。
对角线
棱柱中不在同一平面上的两个顶点的连线叫做棱柱的对角线。
高
棱柱的两个底面的距离叫做棱柱的高。
对角面
棱柱中过不相邻的两条侧棱的截面叫做棱柱的对角面。
体积
假设一个棱柱的底面面积为![]() ,高为
,高为![]() ,那么这个棱柱的体积为:
,那么这个棱柱的体积为: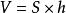 。
。
一些特殊的棱柱
斜棱柱
侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时,一般将侧棱画成不与底面垂直。
直棱柱
侧棱垂直于底面的棱柱叫做直棱柱。画直棱柱时,应将侧棱画成与底面垂直。
正棱柱
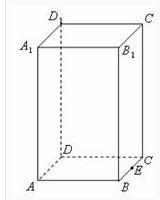 图2.正四棱柱底面是正多边形的直棱柱叫做正棱柱。正棱柱是侧棱都垂直于底面,且底面是正多边形的棱柱。特别注意:底面为正多边形,侧棱垂直于底面,但是侧棱和底面边长不一定相等。而直棱柱侧棱也是垂直于底面,侧棱和底面边长不一定相等,而且底面多边形形状也不确定。[2]
图2.正四棱柱底面是正多边形的直棱柱叫做正棱柱。正棱柱是侧棱都垂直于底面,且底面是正多边形的棱柱。特别注意:底面为正多边形,侧棱垂直于底面,但是侧棱和底面边长不一定相等。而直棱柱侧棱也是垂直于底面,侧棱和底面边长不一定相等,而且底面多边形形状也不确定。[2]
正棱柱性质
(1)正棱柱的侧棱垂直于底面。
(2)正棱柱的侧面与底面相互垂直。
(3)正棱柱的侧面为矩形,但不一定是正方形。[2]

-
上海正艺信息科技有限公司
2025-09-29 08:05:38 查看详情 -
传吉利与法拉第未来正商定代工等事宜 定名缤瑞COOL
2025-09-29 08:05:38 查看详情 -
传吉利与法拉第未来正商定代工等事宜 吉利KX11最新消息曝光
2025-09-29 08:05:38 查看详情


 求购
求购





