反常积分

定积分的积分区间都是有限的，被积函数都是有界的。但在实际应用和理论研究中，还会遇到一些在无限区间上定义的函数或有限区间上的无界函数，对它们也需要考虑类似于定积分的问题。因此，有必要对定积分的概念加以推广，使之能适用于上述两类函数。这种推广的积分，由于它异于通常的定积分，故称之为广义积分，也称之为反常积分。

反常积分存在时的几何意义：函数与X轴所围面积存在有限制时，即便函数在一点的值无穷，但面积可求。

例如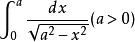的几何意义是：位于曲线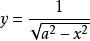之下，X轴之上，直线x=0和x=a之间的图形面积，而x=a点的值虽使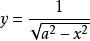无穷，但面积可求。

1.无穷区间反常积分

每个被积函数只能有一个无穷限，若上下限均为无穷限，则分区间积分。

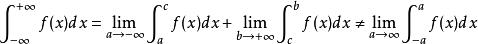
2.无界函数反常积分

即瑕积分，每个被积函数只能有一个瑕点，多个瑕点则分区间积分。

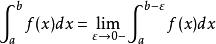（f(b)无界）

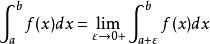（f(a)无界）

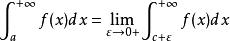（区间内点f(c)无界）

3.混合反常积分

对于上下限均为无穷，或被积分函数存在多个瑕点，或上述两类的混合，称为混合反常积分。对混合型反常积分，必须拆分多个积分区间，使原积分为无穷区间和无界函数两类单独的反常积分之和。

反常积分的敛散判断本质上是极限的存在性与无穷小或无穷大的比阶问题。首先要记住两类反常积分的收敛尺度：对第一类无穷限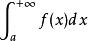而言，当x→+∞时，f(x)必为无穷小，并且无穷小的阶次不能低于某一尺度，才能保证收敛；对第二类无界函数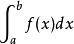而言，当x→a+时，f(x)必为无穷大。且无穷大的阶次不能高于某一尺度，才能保证收敛；这个尺度值一般等于1，注意识别反常积分。