- 赋范线性空间

赋范线性空间
中文名
赋范线性空间
定义
由向量范数诱导出的度量
应用学科
数学术语
概念
赋范线性空间(normed linear space)是在线性空间中引进一种与代数运算相联系的度量,即由向量范数诱导出的度量。赋范线性空间称为Banach空间,是指由范数导出的度量是完备的。
定义:设![]() 是线性空间,函数
是线性空间,函数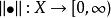 称为
称为![]() 上定义的一个范数,如果满足:
上定义的一个范数,如果满足:
(1)![]() 当且仅当
当且仅当![]() ;
;
(2)对任何![]() 及
及![]() ,
,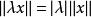 ;
;
(3)对任意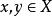 ,
,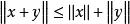 。
。
称二元体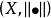 为赋范线性空间。
为赋范线性空间。
在![]() 是赋范线性空间时,由范数导出的度量为
是赋范线性空间时,由范数导出的度量为
![]() 此时
此时![]() 在此度量意义称为度量空间。所以,赋范线性空间是一种特殊的度量空间。点列
在此度量意义称为度量空间。所以,赋范线性空间是一种特殊的度量空间。点列![]() 收敛于
收敛于![]() ,即
,即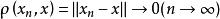 ,有时称这种收敛为依范数收敛。[1]
,有时称这种收敛为依范数收敛。[1]
性质
性质1:设![]() 是赋范线性空间,
是赋范线性空间,![]() ⊂
⊂![]() ,
,![]() ,若
,若![]() ,则
,则![]() 是有界点列。
是有界点列。
证: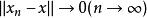 ,对
,对![]() ,存在自然数
,存在自然数![]() ,当
,当![]() 时,
时,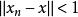 。于是
。于是
![]() 令
令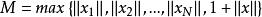 ,那么对一切自然数
,那么对一切自然数![]() ,均有
,均有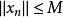 ,即
,即![]() 有界。证毕。
有界。证毕。
性质2:设![]() 中点列
中点列![]() ,
,![]() 及数域
及数域![]() 中数列
中数列![]() 满足
满足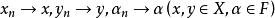 ,则
,则
(1)加法连续: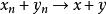 ,即
,即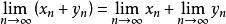 ;
;
(2)数乘连续: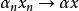 ,即
,即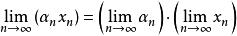 。
。
证:(1)由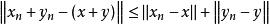 ,得
,得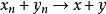 。
。
(2)因![]() ,由性质1,
,由性质1,![]() 有界,所以存在常数
有界,所以存在常数![]() ,满足
,满足 。于是
。于是
![]()
![]()
![]()
![]() 故
故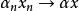 。证毕。[1]
。证毕。[1]

相关百科
-
实拍江铃新宝典(图文) 空间满足家用
2025-09-16 16:22:19 查看详情 -
江铃皮卡赋能用户的美好生活 9万元创富神车开回家
2025-09-16 16:22:19 查看详情 -
江铃域虎7商乘全能铸就经典 空间满足家用
2025-09-16 16:22:19 查看详情 -
江铃福特科技这次是真拼了 江铃皮卡赋能用户的美好生活
2025-09-16 16:22:19 查看详情 -
江铃皮卡赋能用户的美好生活 实拍江铃新宝典(图文)
2025-09-16 16:22:19 查看详情 -
江铃福特轻客持续打造最优TCO 空间满足家用
2025-09-16 16:22:19 查看详情 -
江铃皮卡赋能用户的美好生活 续航里程252km
2025-09-16 16:22:19 查看详情 -
江铃皮卡赋能用户的美好生活 穿山越岭运输专家
2025-09-16 16:22:19 查看详情


 求购
求购



