- 三阶幻方

三阶幻方
基本型
相传, 大禹治水时, 洛水中出现了一个“神龟”背上有美妙的图案,史称“洛书”,用现在的数字翻译出来,就是三阶幻方。
 2500年前,孔子在他研究《易经》的著作《系词上传》中记载了:“河出图,洛出书,圣人则之。”最早将数字与洛书相连的记载是2300年前的《庄子·天运》,它认为:“天有六极五常,帝王顺之则治,逆之则凶。九洛之事,治成德备,监照下土,天下戴之,此谓上皇。”明代数学家程大位在《算法统宗》中也曾发出“数何肇?其肇自图、书乎?伏羲得之以画卦,大禹得之以序畴,列圣得之以开物”的感叹,大意是说,数起源于远古时代黄河出现的河图与洛水出现的洛书,伏羲依靠河图画出八卦,大禹按照洛书划分九州,并制定治理天下的九类大法,圣人们根据它们演绎出各种治国安邦的良策,对人类社会与自然界的认识也得到步步深化。大禹从洛书中数的相互制约,均衡统一得到启发而制定国家的法律体系,使得天下一统,归于大治,这是借鉴思维的开端。这种活化思维的方式已成为科学灵感的来源之一。从洛书发端的幻方在数千年后的今天更加生机盎然,被称为具有永恒魅力的 数学问题。十三世纪,中国南宋数学家 杨辉在世界上首先开展了对幻方的系统研究,欧洲十四世纪也开始了这方面的工作。著名数学家费尔玛、欧拉都进行过幻方研究,如今,幻方仍然是组合数学的研究课题之一,经过一代代数学家与数学爱好者的共同努力,幻方与它的变体所蕴含的各种神奇的科学性质正逐步得到揭示。目前,它已在组合分析、实验设计、图论、数论、群、对策论、纺织、工艺美术、程序设计、 人工智能等领域得到广泛应用。1977年,4阶幻方还作为人类的特殊语言被美国 旅行者1号、2号飞船携入太空,向广袤的宇宙中可能存在的外星人传达人类的文明信息与美好祝愿!
2500年前,孔子在他研究《易经》的著作《系词上传》中记载了:“河出图,洛出书,圣人则之。”最早将数字与洛书相连的记载是2300年前的《庄子·天运》,它认为:“天有六极五常,帝王顺之则治,逆之则凶。九洛之事,治成德备,监照下土,天下戴之,此谓上皇。”明代数学家程大位在《算法统宗》中也曾发出“数何肇?其肇自图、书乎?伏羲得之以画卦,大禹得之以序畴,列圣得之以开物”的感叹,大意是说,数起源于远古时代黄河出现的河图与洛水出现的洛书,伏羲依靠河图画出八卦,大禹按照洛书划分九州,并制定治理天下的九类大法,圣人们根据它们演绎出各种治国安邦的良策,对人类社会与自然界的认识也得到步步深化。大禹从洛书中数的相互制约,均衡统一得到启发而制定国家的法律体系,使得天下一统,归于大治,这是借鉴思维的开端。这种活化思维的方式已成为科学灵感的来源之一。从洛书发端的幻方在数千年后的今天更加生机盎然,被称为具有永恒魅力的 数学问题。十三世纪,中国南宋数学家 杨辉在世界上首先开展了对幻方的系统研究,欧洲十四世纪也开始了这方面的工作。著名数学家费尔玛、欧拉都进行过幻方研究,如今,幻方仍然是组合数学的研究课题之一,经过一代代数学家与数学爱好者的共同努力,幻方与它的变体所蕴含的各种神奇的科学性质正逐步得到揭示。目前,它已在组合分析、实验设计、图论、数论、群、对策论、纺织、工艺美术、程序设计、 人工智能等领域得到广泛应用。1977年,4阶幻方还作为人类的特殊语言被美国 旅行者1号、2号飞船携入太空,向广袤的宇宙中可能存在的外星人传达人类的文明信息与美好祝愿!
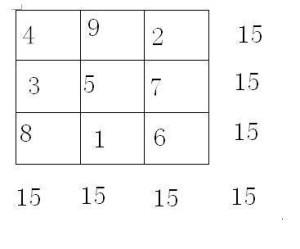
由1、2、3、……等 连续自然数生成的幻方为 基本幻方,在此基础上各数再加或减一个相同的数,可组成由零或 负数组成的新幻方,新 幻方的幻和也随之变化,不再与原幻方幻和同。
如上图基本幻方中各数减1生成的新幻方,幻和为12,如下图示:
构造
拆填方式
 数学术语(3)想:1+9=10,2+8=10,3+7=10,4+6=10。这每对数的和再加上5都等于15,可确定中心格应填5,这四 组数应分别填在横、竖和 对角线的位置上。先填四个角,若填两对奇数,那么因三个奇数的和才可能得奇数,四边上的 格里已不可再填奇数,不行。若四个角分别填一对 偶数,一对奇数,也行不通。因此,判定四个角上必须填两对偶数。对角线上的数填好后,其余格里再填奇数就很容易了。
数学术语(3)想:1+9=10,2+8=10,3+7=10,4+6=10。这每对数的和再加上5都等于15,可确定中心格应填5,这四 组数应分别填在横、竖和 对角线的位置上。先填四个角,若填两对奇数,那么因三个奇数的和才可能得奇数,四边上的 格里已不可再填奇数,不行。若四个角分别填一对 偶数,一对奇数,也行不通。因此,判定四个角上必须填两对偶数。对角线上的数填好后,其余格里再填奇数就很容易了。
古代方式
南宋数学家 杨辉概括的构造方法为:
“九子斜排。上下对易,
左右相更。四维突出。”
中国古代九宫格的填法口诀是:
九宫之义, 法以灵龟,
二四为肩, 六八为足,
左七右三, 戴九履一,
五居中央。
也有把这两者综合起来说的:
九子斜排,上下对易,
左右相更,四维挺出,
戴九履一,左七右三,
二四为肩,六八为足
即:
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
或
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
奇阶幻方通用构造法
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
旋转情况
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
特殊数组
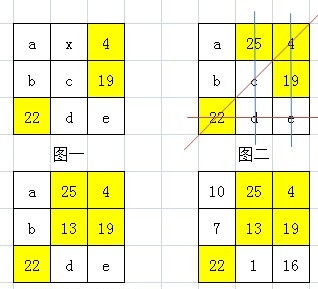 三阶幻方(3)口诀: 1 居上行正中央,
三阶幻方(3)口诀: 1 居上行正中央,
依次斜填切莫忘,
上出框界往下写,
右出框时左边放,
重复便在下格填,
出角重复一个样。
解释:
1)在第一行居中的方格内放1,依次向右上方填入2、3、4…;
2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;
3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;
4)如果右上方已有数字和出了 对角线,则向下移一格继续填写。
5)也可将所填数在幻方中所对应的数填在幻方中对应的位置。
例如:1为第一行中间数,则将对应的9填在最后一行的中间。2以次类推。
按照这种方式,做镜像或旋转对称,可得到实际相同的其他填法: 只要将1放于四个变格的正中,向幻方外侧依次斜填其余数字;若出边,将数字调到另一侧;若目标格已有数字或出角,回一步填写数字,再继续按一开始的相同方向依次斜填其余数字。
任意等差数列
用1~9填出的三阶基本幻方的所有情况都是相互镜像或旋转的。 是本质相同的不同表现:
第一种:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
第二种:
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
第三种:
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
第四种:
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
第五种:
| 6 | 7 | 2 |
| 1 | 5 | 9 |
| 8 | 3 | 4 |
第六种:
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
第七种:
| 2 | 7 | 6 |
| 9 | 5 | 1 |
| 4 | 3 | 8 |
第八种:
| 4 | 3 | 8 |
| 9 | 5 | 1 |
| 2 | 7 | 6 |
等差的三组等差
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
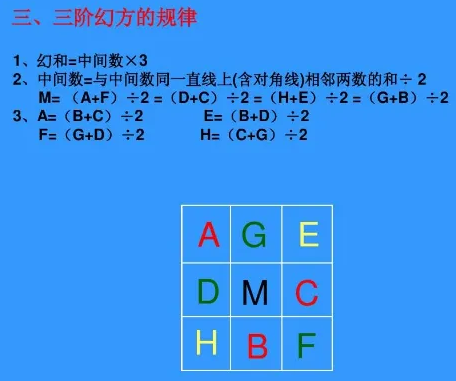
规律
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
幻和与中心数
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
过中心的线
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
边角关系
| 6 | 7 | 2 |
| 1 | 5 | 9 |
| 8 | 3 | 4 |
词条图册
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |

-
长城汽车蜂巢传动邳州基地投产 长城发布自主首个高阶动力总成
2025-09-30 21:17:40 查看详情 -
长城炮全新车型将于成都车展首发 长城发布自主首个高阶动力总成
2025-09-30 21:17:40 查看详情 -
长城山海炮开启量产 长城发布自主首个高阶动力总成
2025-09-30 21:17:40 查看详情 -
长城潮派官图发布 长城发布自主首个高阶动力总成
2025-09-30 21:17:40 查看详情 -
牛津中阶英汉双解词典
2025-09-30 21:17:40 查看详情


 求购
求购





