塑性势

在德鲁克公设（Drucker postulate）提出来之前，人们并不了解塑性应变增量与加载面有什么关系，在1928年Mises类比了弹性应变可用弹性势对应力求偏导的表达式，提出了塑性势的概念，其数学形式是

式中 g 是塑性势函数，它是应力 σij和内变量 ζβ的标量函数，在屈服和硬化为各向同性的情况下，它可以表示为应力不变量和内变量的函数。式中左侧分量表示的单位体积的弹性应变能。1957年布兰德 (D.R.Bland)证明，塑性势和米泽斯屈服函数是同一函数，因此也称为米泽斯屈服函数。据此，可导出普朗特-罗伊斯函数，通过用f(σij)作为塑性势g，可使米泽斯屈服条件与增量理论以更加一般的形式联系起来。 屈服函数f(σij)作为塑性势，可得应力点屈服后产生的塑性应变增量构成的合成向量同f(σij) 曲面上该应力点的外法线方向一致。

对于服从德鲁克公设的稳定材料而言，应取屈服函数 f 作为塑性势函数 g，即取 g=f，这样就将屈服函数与塑性本构关系联系起来考虑。一般地，将 g=f 的塑性本构关系称之为与屈服函数相关联的流动法则，若 g≠f 则称之为非关联的流动法则。在非关联的流动法则下，塑性应变增量与屈服面不正交。非稳定材料如岩土材料的塑性本构关系一般认为服从非关联的流动法则。

在塑性位势理论中，塑性应变率分量（或无限小塑性应变率）的比例关系定义为

式中，g 和 h 均为应力偏量不变量的函数；f 为屈服函数（如果 df=0 ，表示中性加载，则 df<0 表示卸载）；函数 g 称为塑性位势。尽管上式以率的形式给出，但它并不表示真正的时间概念。

假设 g=f ，则上式变为

式中，dλ 为一非负比例常数，等于 hdf 。上式表示了与屈服函数f(σij) 相关的流动规则。

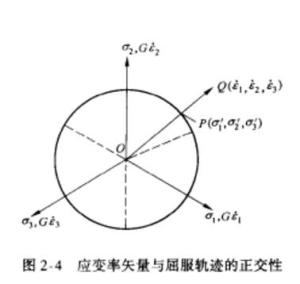
将应力空间 σij与塑性形变空间的坐标重合，并引入一个因子G，G 的大小使得塑性应变率矢量的度量七点位于屈服面上，由于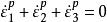，即塑性体积不变条件，则塑性应变率矢量必位于π平面内。同时，因为表示屈服表面f(σij)=C 的外法线方向余弦，则该塑性应变率矢量必然垂直于点（σ'1，σ'2，σ'3）处的屈服轨迹。如右图所示，PO代表塑性应变率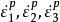（）矢量，它垂直于P点的米席斯屈服圆。塑性位势的概念及其相关的流动法则也可用于屈雷斯加屈服条件。应当注意，若对于给定的塑性应变率存在唯一对应的应力时，则屈服轨迹必须处处外凸。