- 对偶图

对偶图
中文名
对偶图
属性
图论里的概念
相关概念
连通图
概念
设G是平面图,在图G的每个面中指定一个新结点,对两个面公共的边,指定一条新边与其相交。由这些新结点和新边组成的图称为G的对偶图![]() 。[2]
。[2]
例1 图1的图(b)中的虚线是图(a)的对偶图。[3]
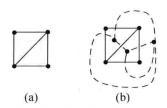 图1
图1
例2 图2的图(b)中的虚线是图(a)的对偶图。[3]
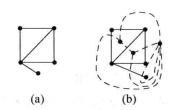 图2
图2
构造方法
给定平面图G,用如下的方法构造G的对偶图![]() :[2]
:[2]
1)在G的每一个面![]() 中任取一个结点
中任取一个结点![]() 作为
作为![]() 的结点;
的结点;
2)若![]() 是G的两个面
是G的两个面![]() 和
和![]() 的公共边.有一条边
的公共边.有一条边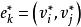 作为
作为![]() 的边,且
的边,且![]() 与
与![]() 相交;
相交;
3)若![]() 只是G的一个面
只是G的一个面![]() 的边界时.以
的边界时.以![]() 中的结点
中的结点![]() 为结点做环
为结点做环![]() 、
、![]() 与
与![]() 相交,
相交,![]() 是
是![]() 的一个环。
的一个环。
性质
(1)如果G是一个连通图且G'是G的对偶图,则G 也是G'的对偶图。[4]
(2)同构平面图的对偶图不一定是同构的。G的对偶图的对偶图也不一定与G同构。
(3)设n、e、f分别为平面图G的结点数、边数和面数,![]() 、
、![]() 、
、![]() 分别为G的对偶图
分别为G的对偶图![]() 的结点数、边数和面数.按照对偶图的定义有
的结点数、边数和面数.按照对偶图的定义有![]() 、
、![]() 、
、![]() 。
。
(4)若与G同构,称G自对偶(self dual)。
(5)任何平面图G的对偶图都是连通的。
(6)若边e为G中的环,则它对应的边为的割边;若边e为G中的割边,则为的环;
(7)G存在唯一的对偶图;
如图3、4所示图G,以虚线为边的图即为G的对偶图。
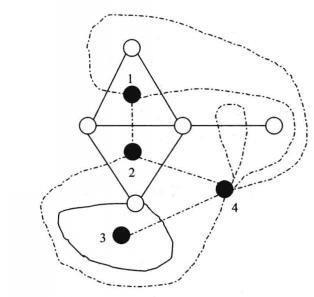 图3
图3
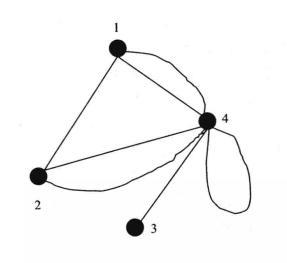 图4
图4

相关百科
-
最新官图发布/将于年内上市 承载式车身结构/年内正式上市
2025-09-22 02:26:38 查看详情 -
Edition上市 全新奔腾B70官图曝光
2025-09-22 02:26:38 查看详情 -
黄海纯电轿车Smile将于12月上市 极氪009实车图曝光
2025-09-22 02:26:38 查看详情 -
路特斯ELETRE将于今日上市 蔚来EC6申报图曝光
2025-09-22 02:26:38 查看详情 -
江南U2正式上市 新款东风风行菱智M5官图发布
2025-09-22 02:26:38 查看详情 -
长安凯程GDI双侠成都上市 新款星途揽月官图
2025-09-22 02:26:38 查看详情 -
款帝豪GL将于3月25日正式上市 2023款奇瑞小蚂蚁官图
2025-09-22 02:26:38 查看详情 -
小鹏全新P7i将于今日上市 2023款奇瑞小蚂蚁官图
2025-09-22 02:26:38 查看详情 -
计划第三季度上市 2023款奇瑞小蚂蚁官图
2025-09-22 02:26:38 查看详情 -
风光SUV首付真0元 名图纯电动轻松拥有
2025-09-22 02:26:38 查看详情


 求购
求购

