剩余类

剩余类亦称同余类。数论的基本概念之一，指全体整数按照对一个正整数的同余关系而分成的类。

设 m 是给定的正整数，以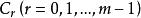表示所有形如的整数组成的集合，其中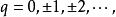则称为模 m 的剩余类。

一个整数被正整数n除后，余数有n种情形：0，1，2，3，…，n-1，它们彼此对模n不同余。这表明，每个整数恰与这n个整数中某一个对模n同余。这样一来，按模n是否同余对整数集进行分类，可以将整数集分成n个两两不相交的子集。我们把（所有）对模n同余的整数构成的一个集合叫做模n的一个剩余类。

模 m 的剩余类具有性质：

1、每一个整数恰包含在某一个类 C_j里(0≤j≤m-1)；

2、两个整数 x，y属于同一类的充分必要条件是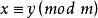。^[1]

由此可引出抽象代数中重要的概念，如群论中的陪集，环论中的剩余类等。任取n，这n个数0，1，…，n-1称为模n的一个完全剩余系。每个数称为相应类的代表元。最常用的完全剩余系是{0，1，…，n-1}。

1、若，则n个整数 ，构成一个完全剩余系的充分必要条件是这n个除n的余数两两不相等。

2、若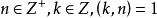，当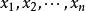为完全剩余系时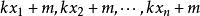，也为完全剩余系。

3、若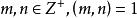，则当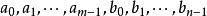是完全剩余系时，

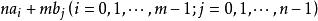也构成完全剩余系。

在个剩余类选取一个与n互素代表元构成简化剩余系。

1、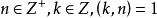，当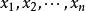为简化剩余系时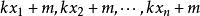，也为简化剩余系。

2、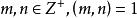则当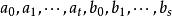是简化剩余系时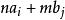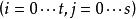，也构成简化剩余系。