分数维度

一个正方形，将它的一部分（边长）扩大

倍后，和原来相似，而且相当于

个小正方形。

同样的，一个正方体的一部分（边长）扩大

倍后，和原来相似，而且相当于

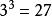个小正方体。

注意指数，和平常的拓扑维一样。

推广一下。l是放大为几倍。d就是拓扑维。

现在把该式改写一下：

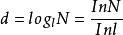。理解它需要具备对数的知识。

那么d脱离了整数的限制，变成分数会怎样？就成为了分维。

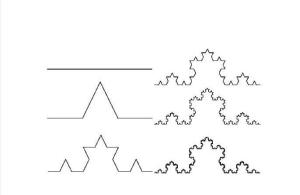它表征分形在通常的几何变换下具有不变性,即标度无关性。由自相似性是从不同尺度的对称出发,也就意味着递归。线性分形又称为自相似分型。自相似原则和迭代生成原则是分形理论的重要原则。分形形体中的自相似性可以是完全相同,也可以是统计意义上的相似。标准的自相似分形是数学上的抽象,迭代生成无限精细的结构,如科契(Koch)雪花曲线、谢尔宾斯基(Sierpinski)地毯曲线等。这种有规分形只是少数,绝大部分分形是统计意义上的无规分形。