- 正十二面体

正十二面体
性质
面的图形:正五边形[1]
面的数目:12
边的数目:30
顶点数目:20
二面角角度: 如果正十二面体棱长为a:
如果正十二面体棱长为a:
表面积: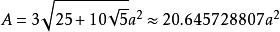
体积: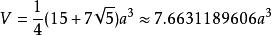
外接球半径: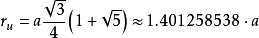
内切球半径: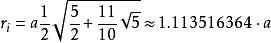
中交球半径: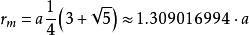
- 我们亦可以将上述三式写作:
外接球半径: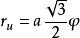
内切球半径: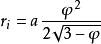
中交球半径: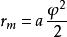
(在这里φ是黄金分割数,φ=![]() )
)
注意到棱长为a的正十二面体的外接球同样外接于棱长为φa的立方体,并且其内切球半径(也即面心距)等于棱长为φa的正五边形的边心距。
对偶多面体:正二十面体
坐标系
如果我们以正十二面体的形心为原点建立三维直角坐标系,那么其20个顶点可被描述为:[2]
(0,±φ,±1/φ)
(±1/φ,0,±φ)
(±φ,±1/φ,0)
(±1,±1,±1)
其中φ = (1+√5)/2,是黄金分割数,也被写作τ,约等于1.618。
该正十二面体棱长为/φ=√5–1。其内接球半径正好为√3。
顶点坐标: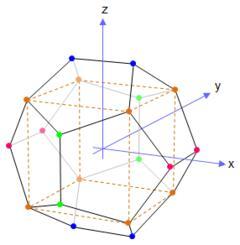 |
|
| 橙色的顶点位于(±1, ±1, ±1),形成了其一个内接立方体(虚线所示)。 | |
| 绿色的顶点位于(0, ±φ, ±1/φ),形成了y–z平面上的一个黄金矩形。 | |
| 蓝色的顶点位于(±1/φ, 0, ±φ),形成了x–z平面上的一个黄金矩形。 | |
| 粉色的顶点位于(±φ, ±1/φ, 0),形成了x–y平面上的一个黄金矩形。 | |
| 相邻顶点间的距离是2/φ,顶点到原点的距离是√3. φ= (1 + √5) / 2是黄金分割数。 |
|
几何关联
顶点坐标: |
|
| 橙色的顶点位于(±1, ±1, ±1),形成了其一个内接立方体(虚线所示)。 | |
| 绿色的顶点位于(0, ±φ, ±1/φ),形成了y–z平面上的一个黄金矩形。 | |
| 蓝色的顶点位于(±1/φ, 0, ±φ),形成了x–z平面上的一个黄金矩形。 | |
| 粉色的顶点位于(±φ, ±1/φ, 0),形成了x–y平面上的一个黄金矩形。 | |
| 相邻顶点间的距离是2/φ,顶点到原点的距离是√3. φ= (1 + √5) / 2是黄金分割数。 |
|
相关数学问题
- 正十二面体是一个无穷家族——截顶偏方面体的第3个成员(截顶五偏方面体)。这类多面体可以被看作是将偏方面体在旋转对称轴上的两个相对的顶点截去而成。
- 正十二面体的星形化体构成了4个星形正多面体中的3个。
- 我们可以在正十二面体的20个顶点中选取5组这样的顶点,使任意两个顶点的连线都是正十二面体正五边形面的一条对角线,这样能构成正十二面体的内接立方体,5个内接立方体一起构成了——复合多面体——五复合立方体;我们还可以进一步对内接立方体做交错操作,得到正十二面体的内接正四面体,如果我们只在内接立方体中取一个正四面体,则5个正四面体构成了有手征性的复合多面体——五复合四面体;如果取两个,则10个正四面体构成了复合多面体——十复合四面体,这三个复合多面体都是正十二面体的小面化体。
- 正十二面体的完全对称群是正二十面体对称群Ih,考克斯特群[5,3],群阶120,还有一个抽象群结构A5×Z2。
- 当正十二面体和正二十面体内接于同一球时,尽管正二十面体有更多的面,但正十二面体占据球的体积(66.49%)要多于正二十面体占据的球的体积(60.54%),这一点与二维不同。
- 棱长相同为1的正十二面体的体积(7.663...)是正二十面体体积(2.181...)的三倍半多。
真实世界
- 哈密顿路径的理论就是源自一个和正十二面体有关的问题:试求一条路径,沿正十二面体的棱经过它所有的顶点。

相关百科
-
双十二魔券降临,江铃皮卡助力暖冬出行 实拍江铃新宝典(图文)
2025-09-28 14:05:10 查看详情 -
双十二魔券降临,江铃皮卡助力暖冬出行 9万元创富神车开回家
2025-09-28 14:05:10 查看详情 -
双十二魔券降临,江铃皮卡助力暖冬出行 低货台更轻松
2025-09-28 14:05:10 查看详情 -
中华人民共和国第十二届全国人民代表大会第三次会议
2025-09-28 14:05:10 查看详情


 求购
求购





