公开密钥加密

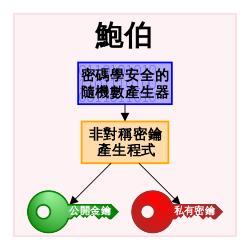非对称加密往往需要密码学安全伪随机数生成器的协助来产生一对密钥，其中一个可以随便公开，称为公钥；另一个不公开，称为私钥，必须由用户自行严格秘密保管，绝不透过任何途径向任何人提供。

如果任何人使用公钥加密明文，得到的密文可以透过不安全的途径（如网络）发送，只有对应的私钥持有者才可以解密得到明文；其他人即使从网络上窃取到密文及加密公钥，也无法（在数以年计的合理时间内）解密得出明文。典型例子是在网络银行或购物网站上，因为客户需要输入敏感消息，浏览器连接时使用网站服务器提供的公钥加密并上传数据，可保证只有信任的网站服务器才能解密得知消息，不必担心敏感个资因为在网络上传送而被窃取。

在现实世界上可作比拟的例子是，一个传统保管箱，开门和关门都是使用同一条钥匙，这是对称加密；而一个公开的邮箱，投递口是任何人都可以寄信进去的，这可视为公钥；而只有邮箱主人拥有钥匙可以打开邮箱，这就视为私钥。

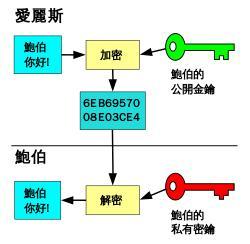在非对称加密中，爱丽丝使用鲍伯的公钥加密明文，得到密文，而只有鲍伯因为持有私钥才可以解密，得到明文。

在数学上，，让我们使用典型的爱丽丝与鲍伯假设来解释：

1. 爱丽丝与鲍伯事先互不认识，也没有可靠安全的沟通渠道，但爱丽丝现在却要透过不安全的互联网向鲍伯发送信息

   爱丽丝撰写好原文，原文在未加密的状态下称之为明文

   鲍伯使用密码学安全伪随机数生成器产生一对密钥，其中一个作为公钥为 ，另一个作为私钥

   鲍伯可以用任何方法发送公钥 给爱丽丝，即使伊夫在中间窃听到 也没问题

   爱丽丝用公钥 把明文 进行加密，得到密文

   爱丽丝可以用任何方法传输密文 给鲍伯，即使伊夫在中间窃听到密文 也没问题

   鲍伯收到密文，用私钥 对密文进行解密 ，得到爱丽丝撰写的明文

   由于伊夫没有得到鲍伯的私钥 ，所以无法得知明文

   如果爱丽丝丢失了她自己撰写的原文 ，在没有得到鲍伯的私钥 的情况下，她的处境将等同伊夫，即无法透过鲍伯的公钥 和密文 重新得到原文

相反，如果某一用户使用他的私钥加密明文，任何人都可以用该用户的公钥解密密文；由于私钥只由该用户自己持有，故可以肯定该文件必定出自于该用户；公众可以验证该用户发布的数据或文件是否完整、中途有否曾被篡改，接收者可信赖这条信息确实来自于该用户，该用户亦无法抵赖，这被称作数字签名，大部分国家已经立法承认数字签名拥有等同传统亲笔签名的法律效力。公钥可以透过数字证书认证机构签授的电子证书形式公布，接收者透过信任链形成一套完整的公开密钥基础建设。例如，从网上下载的安装程序，一般都带有程序制作者的数字签名，可以证明该程序的确是该作者（公司）发布的而不是第三方伪造的且未被篡改过（身份认证/验证）。而在网络银行或购物网站，一般也会使用HTTPS，避免沟通过程中的信息泄露。

对称密钥加密牵涉到密钥管理的问题，尤其是密钥交换，它需要作者和读者在通信之前先透过另一个安全的渠道交换共用的密钥，才可以安全地把密文透过不安全的渠道发送；对称密钥一旦被窃，其所作的加密将即时失效；而在互联网，如果通信双方分隔异地而素未谋面，则对称加密事先所需要的“安全渠道”变得不可行；非对称加密则容许加密公钥随便散布，解密的私钥不发往任何用户，只在单方保管；如此，即使公钥在网上被截获，如果没有与其匹配的私钥，也无法解密，极为适合在互联网上使用。

另一方面，公钥解密的特性可以形成数字签名，使数据和文件受到保护并可信赖；如果公钥透过数字证书认证机构签授成为电子证书，更可作为数字身份的认证，这都是对称密钥加密无法实现的。

不过，公钥加密在在计算上相当复杂，性能欠佳、远远不比对称加密；因此，在一般实际情况下，往往通过公钥加密来随机创建临时的对称秘钥，亦即对话键，然后才通过对称加密来传输大量、主体的数据。

该思想最早由瑞夫·墨克（Ralph C. Merkle）在1974年提出，之后在1976年。惠特菲尔德·迪菲（Whitfield Diffie）与马丁·赫尔曼（Martin Hellman）两位学者以单向函数与单向暗门函数为基础，为发讯与收讯的两方创建密钥。

常见的公钥加密算法有：RSA、ElGamal、背包算法、Rabin（RSA的特例）、迪菲－赫尔曼密钥交换协议中的公钥加密算法、椭圆曲线加密算法（英语：Elliptic Curve Cryptography, ECC）。使用最广泛的是RSA算法（由发明者Rivest、Shmir和Adleman姓氏首字母缩写而来）是著名的公开秘钥加密算法，ElGamal是另一种常用的非对称加密算法。