- 双曲型偏微分方程

双曲型偏微分方程
基本介绍
双曲型偏微分方程简称双曲型方程,是偏微分方程的一种类型。它主要用于描述振动、波动现象与相应的运动过程。它的一个典型特例是波动方程和n=1时的波动方程。可用来描述弦的微小横振动,称为弦振动方程。这是最早得到系统研究的一个偏微分方程。
介定
双曲型方程主要是按偏微分方程的系数特性来介定的。当自变量个数或方程的阶数不同时,双曲型方程可以有不同的定义方式。
二阶线性偏微分方程
对于二阶线性偏微分方程
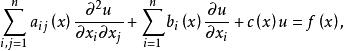 其中,
其中,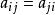 ,则若系数矩阵
,则若系数矩阵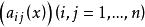 在某点
在某点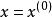 的惯性指数为一正
的惯性指数为一正![]() 负,或一负
负,或一负![]() 正,就称该方程在
正,就称该方程在![]() 点为双曲型的。如果该偏微分方程在区域
点为双曲型的。如果该偏微分方程在区域![]() 中每一点都是双曲型的,则称该方程在
中每一点都是双曲型的,则称该方程在![]() 中为双曲型的。如果一个二阶偏微分方程在
中为双曲型的。如果一个二阶偏微分方程在![]() 点为双曲型的,则可以通过自变量变化将方程在这一点的主部
点为双曲型的,则可以通过自变量变化将方程在这一点的主部 化为
化为
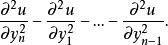 这时变量
这时变量![]() 也常记为 t,称为时间变量。
也常记为 t,称为时间变量。
高阶偏微分方程
对于高阶偏微分方程的情形,为了叙述简明,以下仅对时间方向已确定的情形讨论。在变量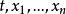 变化的区域
变化的区域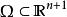 中给定 m 阶偏微分方程
中给定 m 阶偏微分方程
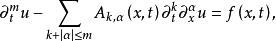 (1)
(1)
其中,k是非负整数,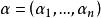 是 n 重指标,若在
是 n 重指标,若在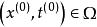 ,对任意的
,对任意的![]() ,特征方程
,特征方程
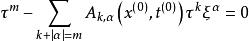 有 m 个不同的实根,则称上述高阶方程为双曲型方程。
有 m 个不同的实根,则称上述高阶方程为双曲型方程。
相应地,可以通过自变量的坐标可以定义关于任意方向的双曲型方程。按上述方式定义的双曲型方程强调了特征方程有 n 个单重实根,它也称为严格双曲型方程 (strictly hyperbolic equation)或称完全双曲型方程,彼得洛夫斯基意义下单双曲方程。
性质
双曲型方程最重要的性质是其柯西问题的适定性。有时人们也用此来作为双曲型方程定义的基础,所以在高阶方程的情形,也有将双曲型方程定义为:若存在常数![]() ,使得对每个
,使得对每个![]() ,包括低次项的关于变量
,包括低次项的关于变量![]() 的方程
的方程
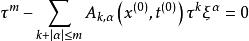 的解必满足
的解必满足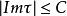 ,则称方程(1)为双曲型方程。这个定义比前一个定义要弱。可以证明,在这样的定义下,双曲型方程柯西问题的适定性仍成立。按这种定义,一个双曲型方程的特征多项式可以允许有多重实根出现,而且方程是否为双曲型与该方程的低阶项有关。
,则称方程(1)为双曲型方程。这个定义比前一个定义要弱。可以证明,在这样的定义下,双曲型方程柯西问题的适定性仍成立。按这种定义,一个双曲型方程的特征多项式可以允许有多重实根出现,而且方程是否为双曲型与该方程的低阶项有关。
对于非线性双曲型方程,双曲型的定义一般要依赖于所考察方程的解。非线性双曲型方程柯西问题光滑的存在性一般只能是局部的。它的解在有限时间内会产生奇性。[1]

-
新款斯巴鲁BRZ上市 雪佛兰开拓者将推5款车型
2025-09-28 20:09:31 查看详情 -
全新紧凑型SUV/上半年上市 别克昂科拉PLUS最新谍照
2025-09-28 20:09:31 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-09-28 20:09:31 查看详情 -
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-09-28 20:09:31 查看详情 -
将于1月6日上市 450六座版车型上市
2025-09-28 20:09:31 查看详情 -
捷途X95热爱Pro版上市 别克微蓝6插混车型上市
2025-09-28 20:09:31 查看详情 -
欧拉闪电猫将于10月31日上市 新增1.5T车型
2025-09-28 20:09:31 查看详情 -
25T车型上市 预售价17.77
2025-09-28 20:09:31 查看详情 -
凯迪拉克CT6新车型上市 W帅气亮相
2025-09-28 20:09:31 查看详情 -
POWER版车型上市 油耗1.7L/100km
2025-09-28 20:09:31 查看详情


 求购
求购

