零因子

众所周知，在数的普通乘法中，如果a≠0，b≠0，则必有ab≠0，但这一性质在一般环中不再成立。

设a≠0是环R的一个元素，如果在R中存在元素b≠0使ab=0，则称a为环R的一个左零因子，同样可定义右零因子。

左、右零因子统称为零因子，只在有必要区分时才加左或右。

既不是左零因子也不是右零因子的元素，称为正则元。^[3]

例1设R为由一切形如

的方阵关于方阵的普通加法与乘法作成的环,其中x，y为有理数，则是R的一个左零因子，因为有

但不是R的右零因子，因为若

则只有。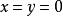

例2数域F上二阶全阵环中，既是左零因子又是右零因子，因为有

数环以及数域上的多项式环，都无零因子。

在无零因子的环中，关于乘法的消去律成立。^[3]

整环阶大于1、有单位元且无零因子的交换环称为整环。

例如，整数环和数域上的多项式环都是整环，而例1和例2中的方阵环都不是整环，整环的定义在不同的书中往往稍有差异，请予留意。

特征数若环R的元素(对加法)有最大阶n，则称n为环R的特征(或特征数)，若环R的元素(对加法)无最大阶，则称R的特征是无限（或零）用char R表示环R的特征。

由于有限群中每个元素的阶都有限，故有限环的元素对加法有最大阶，从而有限环的特征必有限，但是，无限环的特征也可能有限，显然，一阶环即仅包含零元素的环，其特征是1。而在数环中，除去{0}外，其特征均无限。一般来说，环中各元素(对加法)的阶是不相等的，但对无零因子的环来说，这种情况不会发生。^[3]

在环R中，若a不是左零因子，则

若a不是右零因子，则

证明由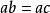得

由于a≠0且a不是左零因子，故b-c=0，b=c。

同理可证另一结论。

如果对环R中任意元素a≠0，b，c，(1)成立，则称环R满足左消去律；若(2)成立，则称R满足右消去律。

若环R无左(或右)零因子，则消去律成立；反之，若R中有一个消去律成立，则R无左及右零因子，且另一个消去律也成立。

证明由于当R无左零因子时，R也无右零因子，故由定理1即得消去律成立，反之，设在R中左消去律成立，且

即

则b=0，即R无左零因子，从而R也无右零因子，于是右消去律也成立。^[3]

设R是一个无零因子环，且，则

1)R中所有非零元素(对加法)的阶均相同；

2)若R的特征有限，则必为素数。

由此定理知，特别地，任何阶大于1的有限环若无零因子，则其特征都是素数。

如果环R的特征是素数p，且R又是一个交换环，则对R中任意元素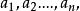必有

这是因为将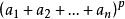展开后，除去项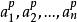外其余各项的系数都是p的倍数，从而都是R的零元。

等式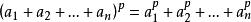显然是与数的普通运算规则很不一样的一个等式。^[3]

当环有单位元时其特征更明显。

若环R有单位元，则单位元在加群(R，+)中的阶就是R的特征。^[3]

证明若单位元1在(R，+)中的阶无限，则R的特征当然无限；若1的阶是正整数n，则在R中任取a≠o，有

即n是R中非零元素的最大阶，亦即