- 摆的等时性原理

摆的等时性原理
详细介绍
如果谁想验证一下摆动的规律,只需找一个适当的支架、一根线和一个钓鱼的铅坠,并将它们如图1所示连接起来就行了.
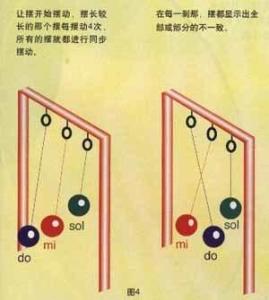 图1
图1
图1
频率增高
频率增高:拉动摆线活动的一头,缩短摆长,摆的频率即随之增高。
轻轻推动摆锤,让其以较小的振幅摆动,然后拉动这根摆线活动的一头,使摆的长度缩短,你就会发现摆动的频率会越来越快。如果摆的长度减小到原来的1/4,摆动的周期就减小1/2倍。当然,如果要想取得准确数据,你就需要对摆动时间进行几十次测量。实验者将会看到,不管是在线上悬挂一个、两个或更多个铅坠,只要线的长度不变,摆的周期就不会发生任何变化.
共振效应
共振效应
摆最重要的特性是它只愿以一种频率,即通常所称的固有频率摆动。当受到外界的干扰而被激励时,它相应的摆动规律则依赖于干扰振频是否和它所希望的一致。这就是人们常说的共振效应。只要当外界的激励和摆的固有频率一致时,才可能将尽可能多的机械能传给摆,道理就在于此。我们可以用一个简单的实验观察共振现象。取一个支架,按图2所示拉一根绳子,在绳子上栓一定数量的摆,其中除了两个摆的长度相等外,其余的均长短不等。绳子的作用是将各个摆“结合”在一起,或者说使其中任何一个摆的摆动能传递到其他摆上去,实际上就是进行干扰和激励。这根绳子能使能量从一个摆传到另一个摆上。
不同摆长的摆:共振现象:使第一个摆摆动起来与它有相同振频的摆也被激励摆动起来。
如果让两个长度相等的摆中的一个开始摆动,就可以看到除了那个同此摆有相同频率的摆以外,其他的摆基本不动。就共振而言,一个摆开始摆动,那么此时激励它的那个摆的摆动就会慢下来,直至停止不动。之后要恢复其摆动,就要以第二个摆为代价,并借助一个摆同另一个摆的机械能相互交替传递来达到。
此处描述的这一原理是乐器发音的基础。在这些乐器中,激励系统是一根弦,而被激励系统则是一个共鸣箱。由振动的弦产生的空气震动可能不足以产生足够的压力波,但如果振动通过琴马传到共鸣箱中去,谐音板开阔的平面就能激励起大量的空气,并发出更强的声音来。
当然,在共鸣箱的诸多固有频率中,琴弦的振动频率是不可缺少的。一把提琴的共鸣箱就是按照能够保障在很宽的频谱范围产生共振的思想设计出来的。像两个配成对的摆一样,声能在共鸣箱和琴弦之间来回传递,这样,对特定琴弦弹拉产生的激励就能够传递到其他任何一根可以用同样频率振动的弦上。例如:在吉他的一根空弦上确定一个“来”(re)音,以便发出“索”(sol)音,这时就可以看到旁边的空弦也开始振动并发出了“索”音。
有一种很好的办法可用来观察这种共振效应。在两根琴弦的每一根弦上都标上一个小白点,将两弦置于放大镜下。当两弦中的某一根弦受到拨弄后,被拨弄的弦上的白点就拉长成一条白线,而此时另一根弦上的白点也随之拉成了一条白线,这就表明另一根弦也被激励起来了。这同两摆的情况完全相同。为了解释乐段中可能出现的和谐音和不和谐音,伽利略在摆与琴弦之间做了类比。从古希腊时代起人们就知道,在多音符的和弦中如果这些音符与基本谐音频率之间的比为小的整数的话,那么这些音符的和弦就是悦耳动听的。比如主音的谐音“多”(do)、“米”(mi)、“索”(SOI)的频率之比为4:5:6(如果换成周期之比,则为1/4:1/5:1/6)。我们还可耳朵偏爱有节奏的给耳膜带来拿三个摆为例,它们分别称为“多”、“米”、“索”,其长度由确定的摆动周期而定(长度之间的比为1/36:l/25:l/16),让它们同时摆动(见图4)。每一个摆都是按照自己的规律摆动,但当最慢的摆每摆动4次时,所有三个摆的摆动也就变得同步了。而如果频率之间的比都是大的整数,那这种情况出现的就比较少了。而如果不是整数的话,那么和谐就无从谈起了。
伽利略的假设是,正如眼睛愿欣赏摆的有条不紊的优雅摆姿一样,耳朵也偏爱各种声音的混合体有节奏地观察共振现象:通过放大镜观察画了小白点的琴弦可以了解琴弦的振动状态。图中显示的是吉他空弦调弦情况。在耳膜上产生同步刺激。音符“多”、“米”、“索”像其他的和谐音一样,其特点是:听觉压力的高峰是按照多音声波的每4个波段为一组一起到来的。相反的情况是,那些振频之间的比例为非小整数的和弦,从来不可能对耳膜产生和谐效应,它产生的只能是不和谐的干扰。这一看法实质上是现代精神听力学家持有的观点,区别在于确定声音是否悦耳与其说是耳膜的问题,还不如说是神经系统的问题。为取得和谐的刺激,耳朵向神经网络发出综台信号,这很简单,也容易解释。这种综合信号比那些杂乱无章的互无关联的信号更受欢迎。但是对有音乐素养的人的耳朵来说,这里也有其特殊性。这类耳朵有能力在和谐的声音结构中去评价不和谐的声音的作用。
声音共鸣
声音共鸣:安东尼奥·斯特拉迪瓦里的一把珍贵的小提琴。琴马是琴弦和共鸣箱之间取得谐振的保障。
现象观察
观察共振现象:
通过放大镜观察画了小白点的琴弦,可以了解琴弦振动状态。
协调一致的摆:如果摆的摆动频率的比为小的整数那么它们就会定时、有规律、协调地摆动。
摆的周期公式
摆的周期公式为:T=2π*根号下L/g.可见,摆的周期与摆长和当地重力加速度有关。

-
460长续航版4月15日上市 提升智能与便捷性
2025-09-28 14:12:27 查看详情 -
定位紧凑级轿车/内上市 提升智能与便捷性
2025-09-28 14:12:27 查看详情 -
V将于6月上市 提升智能与便捷性
2025-09-28 14:12:27 查看详情 -
菱智M5EV长续航版上市 提升智能与便捷性
2025-09-28 14:12:27 查看详情 -
长安福特锐际两驱版本4月17日上市 提升智能与便捷性
2025-09-28 14:12:27 查看详情 -
雪铁龙全新C4正式亮相 可回收材料制造/注重经济性
2025-09-28 14:12:27 查看详情 -
雪铁龙C3L正式亮相 可回收材料制造/注重经济性
2025-09-28 14:12:27 查看详情 -
雪铁龙全新C3L官图泄露 可回收材料制造/注重经济性
2025-09-28 14:12:27 查看详情 -
郎朗喜提沃尔沃XC90 展示可持续性环保材料
2025-09-28 14:12:27 查看详情 -
沃尔沃宣布将推纯电MPV 展示可持续性环保材料
2025-09-28 14:12:27 查看详情


 求购
求购

