向心加速度

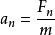
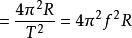
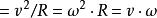
上式中，表示向心加速度，表示向心力，表示物体质量，表示物体圆周运动的线速度（切向速度），表示物体圆周运动的角速度，表示物体圆周运动的周期，表示物体圆周运动的频率，表示物体圆周运动的半径。（=2π/T）

由牛顿第二定律，力的作用会使物体产生一个加速度。合外力提供向心力，向心力产生的加速度就是向心加速度。可能是实际加速度，也可能是物体实际加速度的一个分加速度。

方向始终与运动方向垂直，方向时刻改变且指向圆心，不论加速度的大小是否变化，的方向是时刻改变的，所以圆周运动一定是变加速运动。可理解为做圆周运动物体加速度在指向圆心方向上的分量。

向心加速度是矢量，并且它的方向无时无刻不在改变且指向圆心。

所有做曲线运动的物体都有向心加速度，向心加速度反映的是圆周运动在半径方向上的速度方向(即径向即时速度方向·)改变的快慢。

向心加速度又叫法向加速度，意思是指向曲线的法线方向的加速度。

当物体的速度大小也发生变化时，还有沿轨迹切线方向也有加速度，叫做切向加速度。

向心加速度的方向始终与速度方向垂直，也就是说线速度始终沿曲线切线方向。

①误认为匀速圆周运动的向心加速度恒定不变。实际上，是匀变速运动。合力方向时刻指向圆心，加速度是时刻变化的。

②据公式，误认为与成正比，与半径成反比。事实上，只有在半径确定时才能判断与或与的关系。

向心加速度③向心加速度的公式也适用于非匀速圆周运动，且无论是匀速圆周运动还是非匀速圆周运动，向心加速的的方向都指向圆心。

高一物理《曲线运动》中的“向心加速度”一节，既是教材的重点，也是教材的难点，还是高考的重头戏。

只有认真研究和探索学生在学习“向心加速度”中的困难所在，然后才能做到有的放矢，对症下药。

在本节内容的学习中，学生的疑难点主要有二：一是“既然匀速圆周运动的速度大小不变，却又具有加速度，不好理解”。二是“既然加速度方向指向圆心，物体何不向圆心运动？”学生之所以会产生这样的疑问，是有其认识根源的。

其一，学生对变速直线运动记忆犹新，尤对该运动中“加速度总导致速度大小的改变”印象更为深刻。他们立足于已有的知识和经验来看待匀速圆周运动的加速度，于是难免以老框框套新问题，这种思维定势的负迁移作用，使他们的思维限制在已有的运动模式之中而忽视了问题的不同本质。

其二，学生在此之前虽学习了平抛、斜抛运动，但主要是侧重于运动的合成和分解知识的应用，至于抛体的速度方向何以会时刻改变，它与加速度有怎样的关系，书中并未详述，学生没有建立起较为清晰的模式。他们多数仅仅是从经验出发，被动地接受“物体受到跟速度方向成角度的重力，所以做曲线运动”这一事实。因此可以说他们是在知识准备不足，思维想象无所模拟的情况下来接受新知识的。于是一旦接触到圆周运动，就表现为不能顺应，对于向心加速度感到很抽象，甚至不可思议。

如果我们能在教学之始就注意到这些因素，以指导自己从学生的实际出发，采取相应的方式和方法，对于学生理解和掌握向心加速度的概念，就会收到事半功倍之效。

如何使学生确认匀速圆周运动具有加速度，这是教学中的一个重要环节。笔者的做法是，排除变速直线运动这一思维定势的干扰，用斜上抛运动“搭桥”—一利用斜上抛和圆周运动的速度方向时刻改变这一共性，引导启发学生通过相似联想，从而确认向心加速度的存在。

学生已知斜上抛运动的质点受到单纯重力的作用，具有重力加速度，也知道质点在任一时刻的即时速度方向总是沿着曲线的切线方向。那么其速度方向是怎样改变的呢？为说明这一问题，可画出图1。

对于加速度和速度在同一直线上，只改变速度的大小不改变速度的方向；如果两者有夹角，则一般情况下既改变速度的大小又改变速度的方向，学生已有初步了解。鉴于此，教师可因势利导，将图1中的重力加速度g分解成切向和法向分量(对学生可不言及切向和法向分量名词，只说沿速度方向和垂直于速度方向)。如图2，指出在a、c两点加速度都分解成沿速度方向和垂直于速度方向两个分量，沿速度方向的加速度改变了速度的大小，垂直于速度方向的加速度改变了速度的方向。至于质点在抛物线顶点b时，则因重力加速度与速度方向垂直，全部用来改变速度的方向(为下文推导向心加速度方向埋一伏笔)。这里还要向学生强调：如果没有垂直于速度方向的加速度，则抛体就将沿切线方向飞出而做直线运动。

如上讲解分析之后，再引申过渡到匀速圆周运动，指出一定存在一个使速度方向时刻改变的加速度，否则质点就要沿切线方向飞出而做直线运动，也就顺理成章了。

这里，虽然用到了加速度的分解知识，看似繁琐，甚至有些离题，但实则是避难就易，启发学生通过类比联想，顺乎自然地跨越已有运动模式的困扰，降低了抽象思维的难度，学生易于接受。

在学生已初步认识到匀速圆周运动质点具有使速度方向时刻改变的加速度的基础上，怎样进一步使学生心悦诚服地接受向心加速度的方向“在任一点都沿着半径指向圆心”这一结论，是教学中的又一个环节。

首先，赖于学生对物体做曲线运动的条件的了解，结合上述斜上抛运动速度方向的改变原因(图1、2)，让学生分析得出“向心加速度的方向必指向圆内”，此乃第一步；继而抓住匀速圆周运动的“速度大小不变，方向改变”这一重要特征，启发学生分析思考，欲满足这一条件，则必然在速度方向上没有加速度分量，结合图2质点在抛物线顶点b时的情形得出，“向心加速度在任何一点必定和速度垂直”的结论，此乃第二步；第三步，匀速圆周运动的轨迹是圆，速度方向总沿着圆的切线方向，则垂直于切线的只能是圆的半径。由以上三个特点得出：“质点做匀速圆周运动时，它在任一点的加速度都是沿着半径指向圆心”(并据此画出图3)。故此称为“向心加速度”。是由合外力产生和充当的向心力。

至此，学生对向心加速度的存在及其方向的认识和理解，就不再感到空洞和模糊，而是较为充实和清晰了。

至于向心加速度公式的推导，由于学生的思维已从单纯的抽象概念转变到较能把握住的明晰的空间形象，因此不论是用矢量三角形或其它途径推导公式，学生均不感到困难。笔者的做法是，导出加速度方向后，让学生自己阅读课文，引导和指点他们自己按课本所述矢量三角形法推导出向心加速度公式。尔后再补充介绍一两种其它推导方法(亦可作课后作业留给学生完成)，学生印象更为深刻。本文不再赘述。

通过下面两个问题的探讨和解析，可进一步巩固和深化学生对匀速圆周运动的认识和理解。

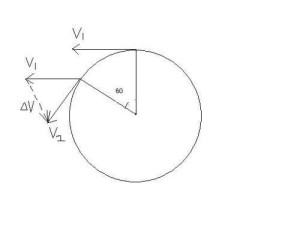
1．向心加速度表征什么意义？

要弄清这个问题，首先要明确矢量三角形中△v的物理意义(图4)

它只表 示速度方向的改变，而不表示速度大小的改变，故而向心加速度所表征的仅仅是速度方向变化的快慢。

2．做匀速圆周运动的物体是否“落”向圆心？

这个问题寓知识于趣味之中，很值得提出来与学生一起探讨，如图5所示，若物体在a点不再具有加速度aa，则物体必将沿ae方向飞出，经t秒后到达e点，而如今物体却“落”到b点上，即离开了ae一段距离eb．当时间t取得足够短时，b点和a点非常接近，且以a点为极限，则可认为ab弧和ab弦互相重合，eb和ad互相重合，且有ab弦=vt，eb=ad．因rt△abc∽rt△adb，则ad/ab=ab/ac，即

由此可见，物体确是时时“落”向圆心，只不过并不能真的到达圆心而已。显然，这是向心加速度导致的结果。

向心加速度公式证明方法（2）并附图

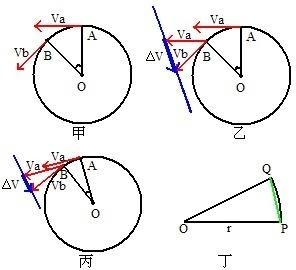证明方法(2)的图片如图甲，一质点绕O点做匀速圆周运动，A点到B点的切线，即线速度Va和Vb，其大小相等。则向心加速度a就是由Vb到Va线速度的单位变化矢量。方法：如图乙，平移矢量Va，使其起点与B点重合，则矢量△V=矢量Vb－矢量Va（即转过某一弧度时线速度的改变量），设矢量Va与Vb的夹角θ就是质点做匀速圆周运动所转过的角（用弧度制表示）。

又如图丁（圆O的一部分，即扇形，OQ=OP=r，同时有弦PQ和弧PQ），设θ为OQ与OP夹角的弧度数（其实是数学上这个角对应的弧长与圆半径的比值，即弧PQ ：半径r的值，如一弧度≈57.3°）那么我们知道 X·Y/X=Y，则弧PQ的长度可以表示为“半径r·弧PQ/半径r”即弧长=半径×对应弧度。 当夹角θ很小很小时，可近似认为弧PQ=弦PQ，也就是说弯曲的弧长与笔直的线段长度几乎一样，这就为后面的求△V提供了依据。

回到图乙，如图当OB,OA之间的夹角（等于Vb与Va的夹角）很小很小时，那么对应的△V就很小很小了，并且以B为顶点，母线长为Va（或Vb）的扇形中由A点到B点所扫过的弧△V就可近似等于弦△V，即根据图丁作介绍的，若把图丁中的半径r看做线速度Va（或Vb），弧长=半径×对应弧度（也就是先前的V=ω·r）用在图乙中就是弧△V=△V=线速度（视为半径r）×弧度θ（弧△V与可视为圆半径r的线速度Va或Vb的比值）

而当△V这个量小到单位时（即一秒钟内△V的量），那么这个△V就是我们所说的向心加速度a，向心加速度a=△V/△t，而弧△V=弦△V，所以向心加速度a=弧△V/△t。

首先弧度θ是质点经过某一时间（△t）做圆周运动所转过的角度的弧度数，则角速度ω=θ/△t，表示一秒钟内转过的弧度数，即弧度θ=ω·△t，①并且△V=弧△V=向心加速度a×△t。②

再根据弧长=半径×对应弧度，弧△V=△V=线速度V×弧度θ（如图丙，当θ小到一定程度时，弧△V=△V，小到单位弧度时就存在这样的关系）再根据①②两式，得出向心加速度a×△t=线速度V（这个矢量的大小始终不变）×角速度ω·△t，同时除去等式左右的△t，于是最终化简为：

向心加速度a=角速度ω×线速度V，即a(n)=ω·V，还有a(n)=ω2·r，a(n)=V^2/r等等 都是根据此式以及V=ω·r推理出来的。