- L-函数
L-函数
函数定义
一般地, 对于数学对象![]() , 我们可定义复数列
, 我们可定义复数列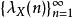 , 形如
, 形如
![]()
且具有Euler乘积的Dirichlet级数, 我们称其为关于![]() 的
的![]() -函数。
-函数。
函数来源
一般地说,![]() -函数来源由两类组成: 算术L-函数和自守L-函数. 这两者又是密切联系在一起的, 根据罗伯特·朗兰兹的猜想, 笼统地说, 一切有意义的L-函数都来自自守L-函数.
-函数来源由两类组成: 算术L-函数和自守L-函数. 这两者又是密切联系在一起的, 根据罗伯特·朗兰兹的猜想, 笼统地说, 一切有意义的L-函数都来自自守L-函数.
算术L-函数
简单地说,
![]()
同样地,狄利克雷在研究算术级数中的素数分布时,引入了Dirichlet L-函数:
![]()
Dedekind zeta-函数: 设![]() 为一代数数域,
为一代数数域,
![]()
椭圆曲线的Haass-Weil L-函数: 设![]() 为一非奇异的椭圆曲线
为一非奇异的椭圆曲线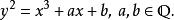 定义
定义![]() 为曲线在有限域
为曲线在有限域![]() 上的解, 设
上的解, 设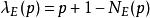 , 则下面的级数称为关于曲线的Haass-Weil L-函数
, 则下面的级数称为关于曲线的Haass-Weil L-函数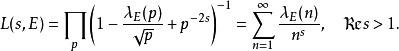
阿廷L-函数: 设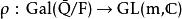 是一个有限维的伽罗瓦表示,其中
是一个有限维的伽罗瓦表示,其中![]() 为一代数数域,
为一代数数域,

自守L-函数
全纯模形式的L-函数, Maass L-函数, 标准L-函数等等[1].
研究内容
根据罗伯特·朗兰兹在国际数学家大会上的报告所指, 研究一个L-函数主要有三部分内容[2]:
解析延拓
L-函数的解析延拓和函数方程这是最基本的一部分. 对于一般的自守L-函数这是较容易得到的, 但是对算术的L-函数这一部分并不是容易得到的. 例如, 对于Haass-Weil L-函数, 这部分就是谷山-志村猜想, 该猜想一部分就能推出费尔马大定理. 关于阿廷L-函数的全纯解析沿拓的阿廷猜想也是数论中重要的未知问题.
对于数学对象![]() 的L-函数, 我们定义其的gamma因子为[3]
的L-函数, 我们定义其的gamma因子为[3]
![]()
其中![]() 为复参数.
为复参数.
![]()
定义下面关于![]() 的完全
的完全![]() -函数
-函数
![]()
那么, 一般地我们有函数方程
![]()
其中![]() 为模为1的复数,
为模为1的复数,![]() 为关于
为关于![]() 的对偶对象.
的对偶对象.
零点的分布
非零区域: 如黎曼zeta函数的目前最好的非零区域为
![]()
黎曼猜想和广义黎曼猜想问题[4]:
在假设黎曼猜想下, 零点虚部的分布问题与随机矩阵的联系等等.
特殊点的值
中心值, 临界点, 整点的值, 极点的留数等. 这里面也有很多猜想, 像BSD猜想, 类数问题, Deligne 猜想,Beilinson 猜想,Goldfeld猜想. 其实往往我们重要的不仅是关心它具体有多大,而是关心的这个量里面隐含着什么样的算术意义。像Dedekind zeta 函数在s=1处的留数,里面包含了一个数域的很多不变量:类数,判别式,regular等;BSD猜想就是Haass-Weil L-函数在中心点的的阶就是该椭圆曲线的秩!
研究意义
对于一个研究对象![]() 如素数, 伽罗瓦扩张, 椭圆曲线, 代数簇等等, 我们可根据其性质构造出一个复变量的L-函数
如素数, 伽罗瓦扩张, 椭圆曲线, 代数簇等等, 我们可根据其性质构造出一个复变量的L-函数![]() . -函数的解析性质: 零点和极点, 函数方程, 展开系数, 特殊点的值等等, 往往能够充分反映
. -函数的解析性质: 零点和极点, 函数方程, 展开系数, 特殊点的值等等, 往往能够充分反映![]() 的算术, 几何, 或代数性质.
的算术, 几何, 或代数性质.
三个公开问题
关于L-函数的研究,有许多未解决的公开问题,在这些问题中,尤以下面三个著名[5].
广义Riemann猜想
L-函数所有非平凡的零点均位于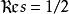 线上.
线上.
广义Lindelof猜想
在(3.1)的函数方程中, 有猜想:
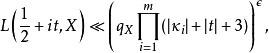
其中![]() 为任意小的正实数.
为任意小的正实数.
广义Ramanujan猜想
在(3.1)的函数方程中,猜想对非分歧的有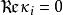 和
和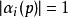 .
.

-
林肯航海家/飞行家百周年限量版上市 吉利豪越L配置曝光
2025-09-19 15:25:05 查看详情 -
内外细节提升/将于近期上市 疑似吉利豪越L路试谍照曝光
2025-09-19 15:25:05 查看详情 -
POWER版车型上市 油耗1.7L/100km
2025-09-19 15:25:05 查看详情 -
长安逸达将于今日上市 别克英朗典范1.5L车型上市
2025-09-19 15:25:05 查看详情 -
珠海英菲尼迪Q50L优惠达5.4万 成都新宝马3系优惠5万元
2025-09-19 15:25:05 查看详情 -
1.5L车型将上市 北京现代第七代伊兰特已下线
2025-09-19 15:25:05 查看详情 -
别克英朗典范1.5L车型上市 6万元
2025-09-19 15:25:05 查看详情 -
预计4月中旬上市 理想L7将于今日上市
2025-09-19 15:25:05 查看详情 -
雪佛兰科鲁泽1.5L四缸车型上市 将于下半年上市
2025-09-19 15:25:05 查看详情 -
1.5L车型将上市 江淮嘉悦X7将于4月20日上市
2025-09-19 15:25:05 查看详情


 求购
求购

