- 换底公式

换底公式
简单介绍
公式
对于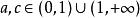 且
且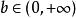 ,有
,有
![]()
推导过程
法一:若有对数![]() ,设
,设![]() ,
,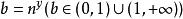 。
。
则根据对数的基本公式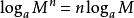 和
和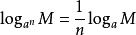 及
及![]() ,
,![]() 可得
可得
![]()
则有
![]()
证毕。
法二:若有对数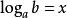 ,则
,则![]() ,且
,且
![]()
于是
![]()
两边取以c为底的对数得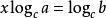 ,
,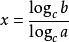 ,即
,即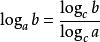 。
。
证毕。
法三:若有对数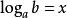 ,则
,则![]() ,且
,且![]() ,于是
,于是
![]()
即
![]()
从而
![]()
证毕。[2]
推论
下面给出若干推论。由换底公式,易知
![]()
![]()
![]()
![]()
![]()
指数函数换底公式
在高等数学中有一种求导方法叫对数求导法,其原理就是指数函数的换底,把底为普通常数或变量的指数函数或幂指函数统统都变形为以e为底的复合函数形式。![]()
这些都可以很容易地由对数换底公式及推论得到。
应用
对数计算
通常在处理数学运算中,将一般底数转换为以e为底的自然对数或者是转换为以10为底的常用对数,方便运算;有时也通过用换底公式来证明或求解相关问题;
在计算器上计算对数时需要用到这个公式。例如,大多数计算器有自然对数和常用对数的按钮,但却没有[log2]的。要计算![]() ,你只有计算
,你只有计算![]() (或
(或![]() ,两者结果一样);
,两者结果一样);
工程技术
在工程技术中,换底公式也是经常用到的公式。
例如,在编程语言中,有些编程语言(例如C语言)没有以a为底b为真数的对数函数,只有以常用对数(即以10为底的对数)或自然对数(即e为底的对数)。此时就要用到换底公式来换成以e或者10为底的对数,表示出以a为底b为真数的对数表达式,从而处理某些实际问题。

相关百科
-
e:PHEV上市 月底正式上市
2025-09-22 15:31:19 查看详情 -
东风标致新408内饰预告图 有望于2月底正式发布
2025-09-22 15:31:19 查看详情 -
07年奥迪a6底盘升降怎么调(奥迪a6l底升怎么调节)
2025-09-22 15:31:19 查看详情 -
Q7发动机机脚怎么换(奥迪q7发动机左机脚胶拆装方法)
2025-09-22 15:31:19 查看详情 -
s挡怎么切换(奥迪a6l(奥迪a6s档怎么用)
2025-09-22 15:31:19 查看详情 -
奥迪a4l如何换空气滤芯(奥迪a4l怎么换空气滤芯)
2025-09-22 15:31:19 查看详情 -
奥迪a6l换音响罩方法(奥迪A6L音响如何拆装)
2025-09-22 15:31:19 查看详情


 求购
求购




