- 格雷码

格雷码
概述
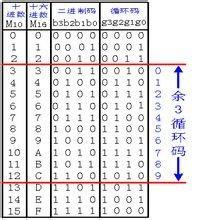 格雷码(4)在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。[3]在数字系统中,常要求代码按一定顺序变化。例如,按自然数递增计数,若采用8421码,则数0111变到1000时四位均要变化,而在实际电路中,4位的变化不可能绝对同时发生,则计数中可能出现短暂的其它代码(1100、1111等)。在特定情况下可能导致电路状态错误或输入错误。使用格雷码可以避免这种错误。格雷码有多种编码形式。
格雷码(4)在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。[3]在数字系统中,常要求代码按一定顺序变化。例如,按自然数递增计数,若采用8421码,则数0111变到1000时四位均要变化,而在实际电路中,4位的变化不可能绝对同时发生,则计数中可能出现短暂的其它代码(1100、1111等)。在特定情况下可能导致电路状态错误或输入错误。使用格雷码可以避免这种错误。格雷码有多种编码形式。
格雷码(Gray Code)曾用过Grey Code、葛莱码、格莱码、戈莱码、循环码、反射二进制码、最小差错码等名字,它们有的不对,有的易与其它名称混淆,建议不要再使用这些曾用名。[4]
码表
格雷码有多种编码形式
| 十进制数 | 4位自然二进制码 | 4位典型格雷码 | 十进制余三格雷码 | 十进制空六格雷码 | 十进制跳六格雷码 | 步进码 |
|---|---|---|---|---|---|---|
| 0 | 0000 | 0000 | 0010 | 0000 | 0000 | 00000 |
| 1 | 0001 | 0001 | 0110 | 0001 | 0001 | 00001 |
| 2 | 0010 | 0011 | 0111 | 0011 | 0011 | 00011 |
| 3 | 0011 | 0010 | 0101 | 0010 | 0010 | 00111 |
| 4 | 0100 | 0110 | 0100 | 0110 | 0110 | 01111 |
| 5 | 0101 | 0111 | 1100 | 1110 | 0111 | 11111 |
| 6 | 0110 | 0101 | 1101 | 1010 | 0101 | 11110 |
| 7 | 0111 | 0100 | 1111 | 1011 | 0100 | 11100 |
| 8 | 1000 | 1100 | 1110 | 1001 | 1100 | 11000 |
| 9 | 1001 | 1101 | 1010 | 1000 | 1000 | 10000 |
| 10 | 1010 | 1111 | ---- | ---- | ---- | ---- |
| 11 | 1011 | 1110 | ---- | ---- | ---- | ---- |
| 12 | 1100 | 1010 | ---- | ---- | ---- | ---- |
| 13 | 1101 | 1011 | ---- | ---- | ---- | ---- |
| 14 | 1110 | 1001 | ---- | ---- | ---- | ---- |
| 15 | 1111 | 1000 | ---- | ---- | ---- | ---- |
表中典型格雷码具有代表性。若不作特别说明,格雷码就是指典型格雷码,它可从自然二进制码转换而来。
特点
| 十进制数 | 4位自然二进制码 | 4位典型格雷码 | 十进制余三格雷码 | 十进制空六格雷码 | 十进制跳六格雷码 | 步进码 |
|---|---|---|---|---|---|---|
| 0 | 0000 | 0000 | 0010 | 0000 | 0000 | 00000 |
| 1 | 0001 | 0001 | 0110 | 0001 | 0001 | 00001 |
| 2 | 0010 | 0011 | 0111 | 0011 | 0011 | 00011 |
| 3 | 0011 | 0010 | 0101 | 0010 | 0010 | 00111 |
| 4 | 0100 | 0110 | 0100 | 0110 | 0110 | 01111 |
| 5 | 0101 | 0111 | 1100 | 1110 | 0111 | 11111 |
| 6 | 0110 | 0101 | 1101 | 1010 | 0101 | 11110 |
| 7 | 0111 | 0100 | 1111 | 1011 | 0100 | 11100 |
| 8 | 1000 | 1100 | 1110 | 1001 | 1100 | 11000 |
| 9 | 1001 | 1101 | 1010 | 1000 | 1000 | 10000 |
| 10 | 1010 | 1111 | ---- | ---- | ---- | ---- |
| 11 | 1011 | 1110 | ---- | ---- | ---- | ---- |
| 12 | 1100 | 1010 | ---- | ---- | ---- | ---- |
| 13 | 1101 | 1011 | ---- | ---- | ---- | ---- |
| 14 | 1110 | 1001 | ---- | ---- | ---- | ---- |
| 15 | 1111 | 1000 | ---- | ---- | ---- | ---- |
发展历史
 格雷码(3)
格雷码(3)
- 格雷码属于可靠性编码,是一种错误很小化的编码方式。因为,虽然自然二进制码可以直接由数/模转换器转换成模拟信号,但在某些情况,例如从十进制的3转换为4时二进制码的每一位都要变,能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点,它在相邻位间转换时,只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。由于这种编码相邻的两个码组之间只有一位不同,因而在用于方向的转角位移量-数字量的转换中,当方向的转角位移量发生微小变化(而可能引起数字量发生变化时,格雷码仅改变一位,这样与其它编码同时改变两位或多位的情况相比更为可靠,即可减少出错的可能性。
- 格雷码是一种绝对编码方式,典型格雷码是一种具有反射特性和循环特性的单步自补码,它的循环、单步特性消除了随机取数时出现重大误差的可能,它的反射、自补特性使得求反非常方便。
- 由于格雷码是一种变权码,每一位码没有固定的大小,很难直接进行比较大小和算术运算,也不能直接转换成液位信号,要经过一次码变换,变成自然二进制码,再由上位机读取。[4]
- 典型格雷码是一种采用绝对编码方式的准权码,其权的绝对值为2^i-1(设最低位i=1)。
- 格雷码的十进制数奇偶性与其码字中1的个数的奇偶性相同。
转换方法
 格雷码(3)法国工程师Jean-Maurice-Émlle Baudot在1880年曾用过的波特码是典型格雷码的一种变形。[4]
格雷码(3)法国工程师Jean-Maurice-Émlle Baudot在1880年曾用过的波特码是典型格雷码的一种变形。[4]
Gray Code是由贝尔实验室的Frank Gray在1940年代提出的,用来在使用PCM(Pusle Code Modulation)方法传送讯号时避免出错。
Frank Gray于1947年申请、1953年获得批准的专利“Pulse Code Communication”,当初是为了通信,后来则常用于模拟-数字转换中。
1941年George Stibitz设计过一种8元格雷码计数器。[4]
递归生成码表
异或转换
这种方法基于格雷码是反射码的事实,利用递归的如下规则来构造:
- 1位格雷码有两个码字
- (n+1)位格雷码中的前2n个码字等于n位格雷码的码字,按顺序书写,加前缀0
- (n+1)位格雷码中的后2n个码字等于n位格雷码的码字,按逆序书写,加前缀1[5]
- n+1位格雷码的集合 = n位格雷码集合(顺序)加前缀0 + n位格雷码集合(逆序)加前缀1
| 2位格雷码 | 3位格雷码 | 4位格雷码 | 4位自然二进制码 |
|---|---|---|---|
| 00 | 000 | 0000 | 0000 |
| 01 | 001 | 0001 | 0001 |
| 11 | 011 | 0011 | 0010 |
| 10 | 010 | 0010 | 0011 |
| 110 | 0110 | 0100 | |
| 111 | 0111 | 0101 | |
| 101 | 0101 | 0110 | |
| 100 | 0100 | 0111 | |
| 1100 | 1000 | ||
| 1101 | 1001 | ||
| 1111 | 1010 | ||
| 1110 | 1011 | ||
| 1010 | 1100 | ||
| 1011 | 1101 | ||
| 1001 | 1110 | ||
| 1000 | 1111 | ||
利用卡诺图
| 2位格雷码 | 3位格雷码 | 4位格雷码 | 4位自然二进制码 |
|---|---|---|---|
| 00 | 000 | 0000 | 0000 |
| 01 | 001 | 0001 | 0001 |
| 11 | 011 | 0011 | 0010 |
| 10 | 010 | 0010 | 0011 |
| 110 | 0110 | 0100 | |
| 111 | 0111 | 0101 | |
| 101 | 0101 | 0110 | |
| 100 | 0100 | 0111 | |
| 1100 | 1000 | ||
| 1101 | 1001 | ||
| 1111 | 1010 | ||
| 1110 | 1011 | ||
| 1010 | 1100 | ||
| 1011 | 1101 | ||
| 1001 | 1110 | ||
| 1000 | 1111 | ||
使用异或乘除
二进制码→格雷码(编码):
此方法从对应的n位二进制码字中直接得到n位格雷码码字,步骤如下:
- 对n位二进制的码字,从右到左,以0到n-1编号
- 如果二进制码字的第i位和i+1位相同,则对应的格雷码的第i位为0,否则为1(当i+1=n时,二进制码字的第n位被认为是0,即第n-1位不变)[5]
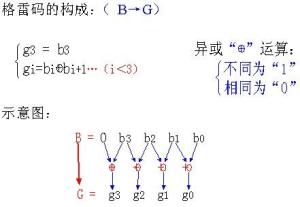 公式表示:
公式表示: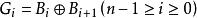 (G:格雷码,B:二进制码)
(G:格雷码,B:二进制码)
例如:二进制码0101,为4位数,所以其所转为之格雷码也必为4位数,因此可取转成之二进位码第五位为0,即0 b3 b2 b1 b0。
0 xor 0=0,所以g3=0
0 xor 1=1,所以g2=1
1 xor 0=1,所以g1=1
0 xor 1=1,所以g0=1
因此所转换为之格雷码为0111
格雷码→二进制码(解码):
从左边第二位起,将每位与左边一位解码后的值异或,作为该位解码后的值(最左边一位依然不变)。依次异或,直到最低位。依次异或转换后的值(二进制数)就是格雷码转换后二进制码的值。
公式表示: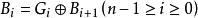 (G:格雷码,B:二进制码)
(G:格雷码,B:二进制码)
原码:p[n:0];格雷码:c[n:0](n∈N);编码:c=G(p);解码:p=F(c);
书写时按从左向右标号依次减小,即MSB->LSB,编解码也按此顺序进行
...................c[n]=p[n],
解码:
应用
利用卡诺图相邻两格只有一位变化以及卡诺图的变量取值以低阶格雷码的顺序排布的特征,可以递归得到高阶格雷码。由于此方法相对繁琐,使用较少。生成格雷码的步骤如下:
- 将卡诺图变量分为两组,变量数目相近(最好相等)
- 以逻辑变量高位在左低位在右建立卡诺图
- 从卡诺图的左上角以之字形到右上角最后到左下角遍历卡诺图,依次经过格子的变量取值即为典型格雷码的顺序
三位格雷码(三位格雷码由建立在二位基础上)
| AB╲ C | 0 | 1 |
| 00 | 0→ | 1↓ |
| 01 | ↓2 | ←3 |
| 11 | 6→ | 7↓ |
| 10 | 4 | ←5 |
格雷码次序:000起点→001→011→010→110→111→101→100终点
四位格雷码
| AB╲CD | 00 | 01 | 11 | 10 |
| 00 | 0→ | 1→ | 3→ | 2↓ |
| 01 | ↓4 | ←5 | ←7 | ←6 |
| 11 | 12→ | 13→ | 15→ | 14↓ |
| 10 | 8 | ←9 | ←11 | ←10 |
格雷码次序:0000起点→0001→0011→0010→0110→0111→0101→0100→1100→1101→
1111→1110→1010→1011→1001→1000终点
角度传感器
| AB╲ C | 0 | 1 |
| 00 | 0→ | 1↓ |
| 01 | ↓2 | ←3 |
| 11 | 6→ | 7↓ |
| 10 | 4 | ←5 |
格雷码
| AB╲CD | 00 | 01 | 11 | 10 |
| 00 | 0→ | 1→ | 3→ | 2↓ |
| 01 | ↓4 | ←5 | ←7 | ←6 |
| 11 | 12→ | 13→ | 15→ | 14↓ |
| 10 | 8 | ←9 | ←11 | ←10 |
九连环问题
用异或代替加减进行二进制竖式乘除,称为异或乘除,它的特点是无进退位。
如:10101除以11将变成1100余1。
二进制转格雷码:
只要异或乘以二分之三,即二进制的1.1,然后忽略小数部分;也可以理解成异或乘以三(即11),再右移一位。
格雷码转二进制:
异或乘以三分之二,即除以1.1,忽略余数;或者左移一位,再异或除以三,忽略余数。
程序实现
词条图册

-
乔治·伯恩斯和格雷西·艾伦秀
2025-09-20 23:50:15 查看详情 -
新帕尔格雷夫经济学大辞典
2025-09-20 23:50:15 查看详情


 求购
求购











