- 函数的相关性

函数的相关性
定义
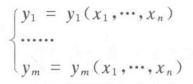 设函数组(如下图)简记作,在的某领域内有定义,又设,则当且仅当存在函数在的任意领域里不恒等为零,使得在的领域里成立时,称为在处函数相关,否则为函数无关。当且仅当在区域(属于)内处处函数相关时,称为在内函数相关。[3]当且仅当在内处处无关时,才称在内函数无关。
设函数组(如下图)简记作,在的某领域内有定义,又设,则当且仅当存在函数在的任意领域里不恒等为零,使得在的领域里成立时,称为在处函数相关,否则为函数无关。当且仅当在区域(属于)内处处函数相关时,称为在内函数相关。[3]当且仅当在内处处无关时,才称在内函数无关。
在区域内处处函数无关时,也可称为函数独立。[4]
判断定理
定理1若雅可比矩阵在点处的秩,则在处函数无关。[3]
 证明因秩,故存在阶的行列式不为零。只要改变一下编号,便可假设行列式(如下图)的值不等于零,根据隐函数存在定理,对于定义中的函数方程组及点存在的领域,使得可写为的函数,适合该函数方程组,且时,(的某一领域)。这表明函数方程组所确定的映射使某领域的像填满了的某个领域,故在处函数无关。[3]
证明因秩,故存在阶的行列式不为零。只要改变一下编号,便可假设行列式(如下图)的值不等于零,根据隐函数存在定理,对于定义中的函数方程组及点存在的领域,使得可写为的函数,适合该函数方程组,且时,(的某一领域)。这表明函数方程组所确定的映射使某领域的像填满了的某个领域,故在处函数无关。[3]
推论:(1)若的雅克比行列式在内处处不等于零,则在内函数无关。即当雅克比行列式(于)时在内函数无关。[3]
(2)若在处函数相关,则矩阵在处秩。[3]
例函数组,的雅可比矩阵(如右下图)中,有一个二阶行列式无零点,所以这两个函数是函数无关的。[3]

定理2设在点的某领域里有连续的一阶偏导数,雅可比矩阵在附近的秩,且这个函数的行列式(如下图)不等于零,则:(1)在处函数无关;(2)在处函数相关。[3]
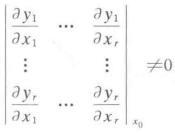
特殊情况
线性代数中,齐次线性函数组的线性相关概念是函数相关的一个特殊情况。注意函数无关性是局部概念,即一组函数在一点无关,而在另一点却函数相关。但线性相关或线性无关则是整体性概念,即在整个空间中,线性函数组要么线性相关,要么线性无关。[1]
由推论1可以得出结论,如果齐次线性函数组函数相关(在某点),则它们必定线性相关(在整个空间上)。[1]
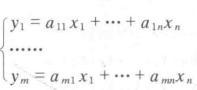 定理3设齐次线性函数组(如右图),则以下三个条件等价:[3]
定理3设齐次线性函数组(如右图),则以下三个条件等价:[3]
(1)在某点处函数相关;(2)线性相关;(3)在中函数相关。[3]
证明(1)=>(2),设(如右下图),因在处函数相关,知在处的秩,从而系数矩阵()的秩,故线性相关。[3]
(2)=>(3),因为线性相关,故存在不全为零的常数使得(于),所以在中处处函数相关。[3]
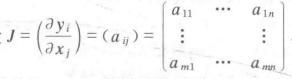 (3)=>(1),明显成立。[3]
(3)=>(1),明显成立。[3]
应用
数据依赖,是指一个关系内部属性与属性之间的一种约束关系。数据依赖主要包括函数依赖(Functional Dependency,简记为FD)和多值依赖,而函数依赖也就是函数的相关性,它描述了一个关系框架的属性之间的联系。例如,假设A和B是关系R的属性,如果A的每个值都与B中的一个值对应,那么B就函数依赖于A(表示为AB)。(A和B均可能由一个或多个属性组成),或者说关系R满足函数相关性XY,其中,X称为FD XY的左边,Y称为右边。[5]
Armstrong公理为一组推理规则,根据该推理规则,可用逻辑推理的方法,由已知成立的一些函数相关性推导出新的函数相关性。[5]

-
460长续航版4月15日上市 提升智能与便捷性
2025-09-23 13:32:36 查看详情 -
定位紧凑级轿车/内上市 提升智能与便捷性
2025-09-23 13:32:36 查看详情 -
V将于6月上市 提升智能与便捷性
2025-09-23 13:32:36 查看详情 -
菱智M5EV长续航版上市 提升智能与便捷性
2025-09-23 13:32:36 查看详情 -
长安福特锐际两驱版本4月17日上市 提升智能与便捷性
2025-09-23 13:32:36 查看详情 -
雪铁龙全新C4正式亮相 可回收材料制造/注重经济性
2025-09-23 13:32:36 查看详情 -
雪铁龙C3L正式亮相 可回收材料制造/注重经济性
2025-09-23 13:32:36 查看详情 -
雪铁龙全新C3L官图泄露 可回收材料制造/注重经济性
2025-09-23 13:32:36 查看详情 -
郎朗喜提沃尔沃XC90 展示可持续性环保材料
2025-09-23 13:32:36 查看详情 -
沃尔沃宣布将推纯电MPV 展示可持续性环保材料
2025-09-23 13:32:36 查看详情


 求购
求购

