- 直线系

直线系
定义
直线系是指具有某种共同特征的直线的集合,表示这个直线系的方程叫做直线系方程,其特点是在直线方程中含有一个参数。
确定平面上一条直线,需要两个独立且相容的几何条件,如果只给定一个条件,直线的位置不能完全确定。另一方面,如果只给定一个几何条件时,二元一次方程的两个独立的系数中,只有一个被确定,那个未被确定的系数是参数。
利用直线系方程求直线,可以简化计算过程,欲求适合某两个几何条件的直线的方程,可先用其中一个条件写出直线系方程,再用另一个条件来确定参数值[2]。
常见的直线系方程
常见的直线系方程有以下几种:
(1)有共同斜率的直线系方程。如斜率为2的直线系方程为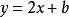 (b为参数)。
(b为参数)。
(2)在![]() 轴上共截距的直线系方程。如截距为3的直线系方程为
轴上共截距的直线系方程。如截距为3的直线系方程为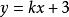 (k为参数)。
(k为参数)。
(3)与直线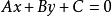 平行的直线系方程为
平行的直线系方程为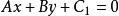 (
(![]() 为参数)。
为参数)。
(4)与直线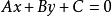 垂直的直线系方程为
垂直的直线系方程为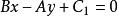 (
(![]() 为参数)。
为参数)。
(5)过已知点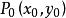 的直线系方程为
的直线系方程为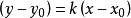 (k为参数),不含直线
(k为参数),不含直线![]() 。
。
(6)过两直线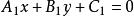 及
及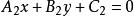 交点的直线系方程为
交点的直线系方程为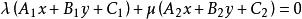 (
(![]() 是不全为零的实数)。
是不全为零的实数)。
(7)在两轴上截距之和为定值p的直线系: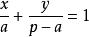 (
(![]() 为参数)。
为参数)。
应用
例1给出两圆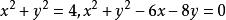 和一点
和一点![]() ,求通过两圆交点和这点的圆。
,求通过两圆交点和这点的圆。
解:不用解联立方程求出两圆交点,再求通过三点的圆,这样做工作量相当大。
凡是通过两已知圆交点的圆的方程必呈下形式
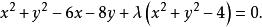 要求此圆通过点
要求此圆通过点![]() 得
得
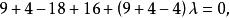 所以
所以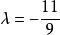 代入上式得所求圆
代入上式得所求圆
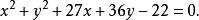
例2求三角形外接圆的方程,已知三角形三边的方程为
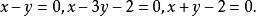
解:按通常的解法,先解三个二元一次方程组,以得出三角形三个顶点的坐标;再按三个条件列出一个三元一次方程组并解出所求圆的系数来,才得出所求圆的方程。
有了直线系和曲线系的启示,这里设计一个新解法:
对于一切实数a和b,二次曲线
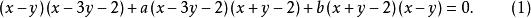 必通过三边两两交点。这是因为:设
必通过三边两两交点。这是因为:设![]() 是一个顶点,以
是一个顶点,以![]() 代替
代替![]() ,它使这里出现的三个不同的括号中的两个为零,因而上式左端三项都为零,可见曲线(1)通过
,它使这里出现的三个不同的括号中的两个为零,因而上式左端三项都为零,可见曲线(1)通过![]() ,即通过任一顶点。
,即通过任一顶点。
进一步要使二次曲线(1)代表圆,二次曲线是圆的充要条件是两条:
(1)![]() 的系数=
的系数=![]() 的系数;
的系数;
(2)![]() 的系数=0[3]。
的系数=0[3]。
于是得
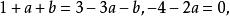 所以
所以
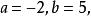 代入式(1),乘出得所求外接圆的方程为
代入式(1),乘出得所求外接圆的方程为
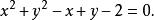

-
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-09-21 17:09:13 查看详情 -
广汽本田全新皓影正式上市 宝马1系M运动曜熠版上市
2025-09-21 17:09:13 查看详情 -
雪佛兰开拓者正式上市 全新宝马7系/i7正式上市
2025-09-21 17:09:13 查看详情 -
珠海英菲尼迪Q50L优惠达5.4万 成都新宝马3系优惠5万元
2025-09-21 17:09:13 查看详情 -
成都新宝马3系优惠5万元 再送装潢礼包
2025-09-21 17:09:13 查看详情 -
i/汉EV创世版有望3月16日上市 中期改款5系再曝光
2025-09-21 17:09:13 查看详情 -
前脸更像7系/或将于中上市 旗下首款纯电动车型
2025-09-21 17:09:13 查看详情 -
成都丰田锐志最高优惠2.7万元 青岛宝马8系现金优惠达9万元
2025-09-21 17:09:13 查看详情 -
斯威G01改款车型将于10月上市 前脸更像7系/或将于中上市
2025-09-21 17:09:13 查看详情 -
前脸更像7系/或将于中上市 3正式在日本上市
2025-09-21 17:09:13 查看详情


 求购
求购

