直线束

平面上的直线束是指平面上通过一个固定点的所有直线的集合，也指平面上平行于一条已知直线的所有直线的集合。第一种情况中，束的所有直线所通过的点叫做束的中心，这个束本身叫做真的；第二种情况中，我们说束的中心“落在无穷远处”，而这个束叫做假的。显然，每一对不重合的直线包含在一个而且只有一个（真的或者假的）束里。^[1]

平面上，一条直线以及平行于这条直线的全体直线的集合叫做平行直线束。^[2]

（1）平行直线束的任何一条直线都可以完全确定这个平行直线束。

（2）由已知直线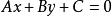确定的平行直线束的方程为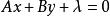：，其中为参数，它可以取任意实数。

（3）垂直于直线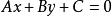的平行直线束的方程为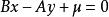：，其中为参数，它可以取任意实数。^[2]

平面上通过某个定点的直线的集合叫做一个中心直线束（简称线束），该定点叫做这个直线束的中心（束心）。中心直线束是平行直线束在某种意义下的特殊情形。^[2]

以点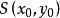为中心的直线束的方程为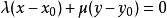：，其中均为参数，它们可以独立地取不同时为0的任意实数。^[2]

中心直线束的两条直线也确定这个直线束。要求这个直线束的方程，可先求出这两条直线的交点，然后按照已知点为中心，求出该直线束的方程。^[2]

设有两条相交直线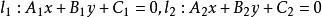，，那么由这两条直线所确定的中心直线束的方程为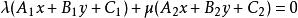：，其中均为参数，它们可以独立地取不同时为0的任意实数。^[2]

直线束可用来求经过两条相交直线交点的某直线的方程，只需用此直线的条件决定式中的比例关系。^[3]