惯性张量

转动惯量(Moment of Inertia)是表征刚体转动惯性大小的物理量，它与刚体的质量、质量相对于转轴的分布有关。

转动惯量是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。 在经典力学中，转动惯量（又称质量惯性矩，简称惯距）通常以I 或J表示，SI 单位为 kg·m²。对于一个质点，I = mr²，其中 m 是其质量，r 是质点和转轴的垂直距离。转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

其量值取决于物体的形状、质量分布及转轴的位置。刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。电磁系仪表的指示系统，因线圈的转动惯量不同，可分别用于测量微小电流（检流计）或电量（冲击电流计）。在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上，精确地测定转动惯量，都是十分必要的。

转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。形状规则的匀质刚体，其转动惯量可直接用公式计算得到。而对于不规则刚体或非均质刚体的转动惯量，一般通过实验的方法来进行测定，因而实验方法就显得十分重要。转动惯量应用于刚体各种运动的动力学计算中。

转动惯量的表达式为

转动惯量的表达式

若刚体的质量是连续分布的，则转动惯量的计算公式可写成

转动惯量的计算公式

(式中mi 表示刚体的某个质元的质量，r表示该质元到转轴的垂直距离,ρ表示该处的密度，求和号（或积分号）遍及整个刚体。)

转动惯量的量纲为[L]^2[M] ，在SI单位制中，它的单位是kg·m^2 。

此外，计算刚体的转动惯量时常会用到平行轴定理、垂直轴定理（亦称正交轴定理）及伸展定则。

有实际应用价值的只是平面积的转动惯量，平面积A对平面内互相垂直的x和y轴的转动惯量分别

为

平面积A对平面内互相垂直的x轴的转动惯量

 和

平面积A对平面内互相垂直的y轴的转动惯量

式中x，y为面元dA的位置坐标。平面积A对于通过x，y轴交点并同它们互相垂直的z轴的转动惯量（又称极转动惯量）为：

极转动惯量

式中为面元dA至z轴的垂直距离（见截面的几何性质）。面积转动惯量常用的单位有厘米和等。

描述面积绕同它垂直的互相平行诸转轴的转动惯量之间的关系有如下的平行轴定理：面积对于一轴的转动惯量，等于该面积对于同此轴平行并通过形心之轴的转动惯量加上该面积同两轴间距离平方的乘积。由于和式的第二项恒大于零，因此面积绕过形心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。^[1]

张量（tensor）是一个定义在的一些向量空间和一些对偶空间的笛卡儿积上的多重线性映射，是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。刚体绕某一点转动的惯性可由更普遍的惯性张量（Inertia tensor）描述。惯性张量（Inertia tensor）是二阶对称张量，它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。出于简单的角度考虑，这里仅给出绕质心的转动惯量张量的定义及其在力矩方程中的表达式。

设有一个刚体A,其质心为C,刚体A绕其质心C的转动惯量张量定义为

转动惯量张量定义

该积分遍及整个刚体A，其中，是刚体质心C到刚体上任一点B的矢径；表达式 是两个矢量的并乘；而为单位张量，标架 是一个典型的单位正交曲线标架； 是刚体的密度。

转动惯量张量的力矩方程

设刚体A所受到的绕其质心C的合力矩矢量为 ，刚体A在惯性系下的角速度矢量为 ，角加速度矢量为 ，A绕其质心的转动惯量张量为 ，则有如下的力矩方程：

将上面的矢量形式的力矩方程向各个坐标轴投影（或者，更确切地说，与各个坐标轴的单位方向矢量相点乘），就可以获得各个坐标轴分量方向的标量形式的力矩方程。

转动惯量张量 是一个二阶张量，虽然在标架 下它有九个分量，但是因为它是一个对称张量，故其实际独立的分量只有六个。^[2]

对于 三维空间中任意一参考点 K与以此参考点为原点的 直角坐标系Kxyz ，一个刚体的惯性张量可以表示为下面的3X3的矩阵

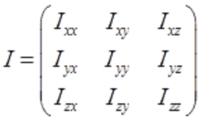
这里，矩阵的对角元素 Ixx、Iyy、Izz分别为对于 x-轴、y-轴、z-轴的 转动惯量。

设定（x,y,z)为微小质量dm对于点K的相对位置。则这些 转动惯量以方程式定义为

Ixx=∫(y*y+z*z)dm

Iyy=∫(x*x+z*z)dm

Izz=∫(x*x+y*y)dm

矩阵的非对角元素，称为 惯性积, 以方程式定义为

Ixy=Iyx=∫x*y dm

Ixz=Izx=∫x*z dm

Iyz=Iyz=∫y*z dm

一质点惯性的度量为该质点的质量。考虑有n个质点构成的质点系。令质点系内任意一质点Pi的质量为mi。对于该质点系，度量其惯性的物理量之一为质点系的总质量，即

质量在国际单位制中单位为千克(kg)。对于刚体，如果将上式的求和号对刚体的所有质点进行，得到刚体的质量。它是刚体平移运动惯性的度量。

现考察质量相同的两个圆环，用同样的力偶绕圆环的轴线驱动它们，发现直径大的圆环启动比较困难，表现出较大的惯性。说明刚体在作转动时，系统的惯性将与质点系的质量的分布有关。为此需引入描述质点系惯量的另一个物理量：

转动惯量

在刚体上过点O建立一连体基(见图5-1)，质点Pk相对于O的矢径为，其在该基上的坐标阵为，定义

其中rkx、rky与rkz分别为质点Pk到Ox、Oy与Oz轴的距离。称JOx、JOy与JOz分别为刚体关于Ox、Oy与Oz轴的转动惯量。转动惯量在国际单位制中单位为千克平方米()。转动惯量的另一种表达方法为

其中，m为刚体的质量，rx、ry与rz分别称为刚体对Ox、Oy与Oz轴的回转半径。一些常见的规则外形均质刚体转动惯量与回转半径见附录A。

惯性积

描述刚体转动惯量的另一个量为刚体的惯性积。对于过刚体上点O的连体基，定义如下与转动惯量有相同量纲的量：

称JOxy与JOyx为刚体关于Oxy平面的惯性积；称JOyz与JOzy为刚体关于Oyz平面的惯性积；JOzx与JOxz为刚体关于Oxz平面的惯性积。

刚体的惯量主轴与主轴连体基

如果惯性积与为零，则称Oz轴为刚体的惯量主轴。同样如果与为零或与为零称Ox轴或Oy轴为刚体的惯量主轴。不难验证，对于有对称轴的刚体，则该对称轴为刚体的主轴；对于有对称面的刚体，垂直于该平面的任意轴为该刚体的主轴。可以证明对于刚体上的点O至少存在一个连体基，该基的三根轴同时为刚体的主轴，该基称为刚体的惯量主轴连体基。关于主轴连体基三轴的转动惯量称为刚体的主转动惯量。过刚体质心的主轴连体基称为中心惯量主轴连体基，关于该基三轴的转动惯量称为刚体的中心主转动惯量。