对角线构图

　　词目：对角线构图
　　拼音：duijiaoxiangoutu
　　释义：是摄影中的术语，是一种构图方法，与黄金构图、水平构图、垂直构图相对应...物体在画幅中两对角的连线，近似于对角线，名由形状来定的。
　　设计中的一种技法，在建筑，美术，工业设计中也广泛使用。

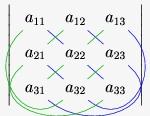　　对角线，几何学名词，定义为连接多边形任意两个不相邻顶点的线段，或者连接多面体任意两个不在同一面上的顶点的线段。另外在代数学中，n阶行列式，从左上至右下的数归为主对角线，从左下至右上的数归为副对角线。
　　由三角形的三个顶点就能确定这个三角形的位置、形状和大小；当没有给出顶点时，由三角形的一些元素（共六个元素，分别为三角形的三条边和三个内角）也能确定三角形的形状和大小。确定了三角形，就能研究这个三角形的中线、高、角平分钱、中位线这几个重要的线段。在四边形中，是通过对角线把它分割成三角形来研究的，这样四边形中的对角线就显得更加重要。本文就如何巧用四边形的对角线来判定特殊的四边形举例加以分析，供同学们学习时参考。一.利用对角线判定特殊的四边形在课堂上我们已探索过以下几个重要的结论：（1）对角线互相平分的四边形是平行四边形；（2）对角线互相平分且相等的四边形是矩形；（3）对角线互相平分且垂直的四边形是菱形；（4）对角线相等且互相垂直平分的四边形是正方形；（5）对角线相等的梯形是等腰梯形。其实以上这些结论是有联系的。如图1，四边形ABCD中，两条对角线相交于点O。（1）当OA=OC，OB=OD时，四边形ABCD是平行四边形。（2）在OA=OC，OB=OD的基础上增加AC=BD条件时，四边形ABCD在平行四边形的基础上变成矩形。（3）在OA=OC，OB=OD的基础上增加ACBD条件时，四边形ABCD在平行四边形的基础上变成菱形。（4）在OA=OC，OB=OD的基础上增加AC=BD，条件时，四边形ABCD在平行四边形的基础上变成正方形。（5）当AB//CD，且，OA=OB时，此时的四边形ABCD为对角线相等的梯形，即等腰梯形。由此可知，把一个一般的四边形变为特殊的四边形，可以通过改变两条对角线的大小关系和位置关系来完成。这也是特殊四边形之间重要的联系纽带之一。二.利用对角线判定动态四边形的形状如图2，中，点O是边AC上的一个动点，P是BC延长线上一点。过点O作直线MN//BC，设MN交∠BCA的平分线于点E，交∠PCA的平分线于点F，连结AE、AF。（1）图中有等腰三角形吗？（2）当点O运动到何处时，四边形AECF是矩形？简要说明理由。（3）在（2）中的矩形可能是正方形吗？此时应满足什么条件？分析：（1）图2中有等腰三角形。理由：是等腰三角形。（2）当点O运动到AC的中点时，四边形AECF是矩形。理由如下：由（1）得。由O是AC的中点，得。所以:所以四边形AECF的两条对角线AC、EF互相平分且相等。故四边形AECF为矩形。所以，当点O运动到AC的中点时，四边形AECF是矩形。（3）在（2）中的矩形可能是正方形。理由：因为MN//BC，当∠ACB=90°时，∠AOE=∠ACB=90°，即对角线AC、EF互相垂直。所以这时四边形AECF是正方形。即在这当中,当∠ACB=90°时，在（2）中的矩形AECF是正方形。