- 海明校验码
海明校验码
基本思想
将有效信息按某种规律分成若干组,每组安排一个校验位,做奇偶测试,就能提供多位检错信息,以指出最大可能是哪位出错,从而将其纠正。实质上,海明校验是一种多重校验。
特点
它不仅具有检测错误的能力,同时还具有给出错误所在准确位置的能力 但是因为这种海明校验的方法只能检测和纠正一位出错的情况。所以如果有多个错误,就不能查出了。 假设为k个数据位设置r个校验位,则校验位能表示2^r个状态,可用其中的一个状态指出 "没有发生错误",用其余的2 ^r -1个状态指出有错误发生在某一位,包括k个数据位和r个校验位,因此校验位的位数应满足如下关系:
2^r ≥ k + r + 1 (2.7)
如要能检出与自动校正一位错,并能同时发现哪位错,此时校验位的位数r和数据位的位数k应满足下述关系:
2^r-1 ≥ k + r (2.8)
按上述不等式,可计算出数据位k与校验位r的对应关系,如表2.2所示。
表2.2
| k值 | 最小r值 |
| 1 | 2 |
| 2~4 | 3 |
| 5~11 | 4 |
| 12~26 | 5 |
| 27~57 | 6 |
| 58~120 | 7 |
分组原则
| k值 | 最小r值 |
| 1 | 2 |
| 2~4 | 3 |
| 5~11 | 4 |
| 12~26 | 5 |
| 27~57 | 6 |
| 58~120 | 7 |
对应关系
在海明码中, 位号数(1、2、3、……、n)为2的权值的那些位,即:
1(2^0)、2(2^1)、4(2^2)、8(2^3)、…2^(r-1)位,作为奇偶校验位,并记作: P1、P2、P3 、P4、…Pr,余下各位则为有效信息位。例如: N=11(海明码位数)K=7(数据位数)r=4(校验位) ,相应海明码可表示位号为: 1, 2, 3, 4 ,5 ,6, 7, 8, 9 ,10 ,11,校验位P占第1,2,4,8位,其他位为有效信息位,海明码中的校验位分别标示为P1,P2,P3,P4… Pr ,并被信息位中的一至若干位所校验,其规律是:第i位,由校验位位号之和等于i的那些校验位所校验,如:海明码的位号为3,它被P1P2(位号分别为1,2)所校验,海明码的位号为5,它被P1P3(位号分别为1,4)所校验。归并起来: 形成了4个小组,每个小组一个校验位,校验位的取值,仍采用奇偶校验方式确定。
设计海明码编码的关键技术,是合理地把每个数据位分配到r个校验组中,以确保能发现码字中任何一位出错;若要实现纠错,还要求能指出是哪一位出错,对出错位求反则得到该位的正确值。例如,当数据位为3位(用D3 D2 D1表示)时,检验位应为4位(用P4 P3 P2 P1表示)。可通过表2.3表示的关系,完成把每个数据位划分在形成不同校验位的偶校验值的逻辑表达式中。
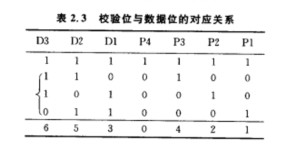
表2.3 校验位与数据位的对应关系
在P1、P2、P3、P4竖列相应行分别填1,
在该4列的低3横行其它位置分别填0,
在最顶横行的每个尚空位置都分别填1。
若只看第3横行,右4竖列的3个bit的组合值分别为十进制的1、2、4、0,则分配 D1 D2 D3列的组合值为3 5 6,保证低3横行各竖列的编码值各不相同。
表中D3 D2 D1为三位数据位,P4 P3 P2 P1为四位校验位。其中低三位中的每一个校验位P3 P2 P1的值,都是用三个数据位中不同的几位通过偶校验运算规则计算出来的。其对应关系是:对Pi(i的取值为1~3),总是用处在Pi取值为1的行中的、用1标记出来的数据位计算该Pi的值。最高一个校验位P4,被称为总校验位,它的值,是通过对全部三个数据位和其它全部校验位(不含P4本身)执行偶校验计算求得的。
形成各校验位的值的过程叫做编码,按刚说明的规则,4个校验位所用的编码方程为:
P4 = D3 D2 D1 P3 P2 P1
P3 = D3 D2
P2 = D3 D1
P1 = D2 D1
由多个数据位和多个校验位组成的一个码字,将作为一个数据单位处理,例如被写入内存或被传送走。之后,在执行内存读操作或在数据接收端,则可以对得到的码字,通过偶校验来检查其合法性,通常称该操作过程为译码,所用的译码方程为:
S4 = P4 D3 D2 D1 P3 P2 P1
S3 = P3 D3 D2
S2 = P2 D3 D1
S1 = P1 D2 D1

-
全自动SF6密度继电器校验仪
2025-10-31 12:39:30 查看详情 -
上海明天广场万豪行政公寓
2025-10-31 12:39:30 查看详情 -
上海明天广场JW万豪酒店
2025-10-31 12:39:30 查看详情


 求购
求购