哈密顿回路

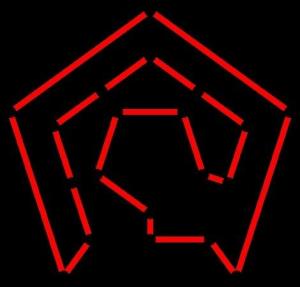哈密顿回路天文学家哈密顿(William Rowan Hamilton) 提出，在一个有多个城市的地图网络中，寻找一条从给定的起点到给定的终点沿 途恰好经过所有其他城市一次的路径。

这个问题和著名的七桥问题的不同之处在于，过桥只需要确定起点，而不用确定终点。哈密顿问题寻找一条从给定的起点到给定的终点沿 途恰好经过所有其他城市一次的路径。

哈密顿路径问题在上世纪七十年代初，终于被证明是“NP完全”的。据说具有这样性质的问题，难于找到一个有效的算法。实际上对于某些顶点数不到100的网络，利用现有最好的算法和计算机也需要比较荒唐的时间（比如几百年）才能确定其是否存在一条这样的路径。

从图中的任意一点出发，路途中经过图中每一个结点当且仅当一次，则成为哈密顿回路。

要满足两个条件：

⒈封闭的环

⒉是一个连通图，且图中任意两点可达

经过图（有向图或无向图）中所有顶点一次且仅一次的通路称为哈密顿通路。

经过图中所有顶点一次且仅一次的回路称为哈密顿回路。

具有哈密顿回路的图称为哈密顿图，具有哈密顿通路但不具有哈密顿回路的图称为半哈密顿图。

平凡图是哈密顿图。

⒊若以1到2、2到3、3到4、4到5、5到1，为计数规律，则各点均出现两次；这种判断方法在计算机编程运算中显得尤为重要，其会精简很多运算过程。

⒋新出炉，有待检测的代码如下：

注：这段代码采用分支定界法作为编写程序的依据，因此代码依旧局限在算法上；而且代码的使用对所要计算的数据是有要求的，如下：

⒈只要数据在开始计算出的n个最小值中，其重复次数超过2次的点的种类只能为一种，例如：代码段中的数据五个最小值中其重复次数超过2次的点只有v5。

⒉数据矩阵格式要求：只允许为上三角矩阵，不支持全矩阵以及下三角矩阵的运算。

⒊代码扩展方法请使用者独立思考，不唯一。

⒋运算数据扩展方法，请使用者独立思考，不唯一。

⒌此代码为本人毕设的附加产品，不会对使用此代码者，因理解不当或使用不当而造成的任何不良后果，付出任何责任。

⒍代码仅供交流。

C代码

#include#include#include#include#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAX_VER_NUM 11//顶点的最大数
#define MAX_ARC_NUM 22//边的最大数
typedef char VertexType;
typedef int Status;
typedef struct EdgeInfo {
    VertexType v1;
    VertexType v2;
    int weight;
}EdgeInfo;
typedef struct ArcBox//边所包含的信息 {
    int iver;
    struct ArcBox *ilink;
    int jver;
    struct ArcBox *jlink;
    int weight;//权值
    int mark;
    char *info;
}ArcBox;
typedef struct VerBox//顶点所包含的信息 {
    VertexType data;//顶点值
    ArcBox *firstedge;//指向邻接点（边所包含的信息）
}VerBox;
typedef struct Graph {
    int vernum;//顶点总个数
    int arcnum;//边的总个数
    VerBox vertexs[MAX_VER_NUM];//顶点信息
}Graph;
typedef struct StackData//栈中可存放的数据 {
    VertexType data;
    int lenght;
    struct StackData *pnext;
}StackData;
typedef struct Stack//栈用于存放已访问过的顶点 {
    struct StackData *ptop;
    struct StackData *pbottom;    
}STNODE;
typedef struct Stack_Arc//存方已访问过的边及顶点 {
    ArcBox *p[MAX_ARC_NUM];
    int v_num[MAX_ARC_NUM];
}SANode;
int Visited[MAX_VER_NUM];//标记顶点是否被访问过
EdgeInfo Data[MAX_ARC_NUM]={{'A','B',324},{'A','J',419},{'A','K',328},{'A','D',241},{'A','C',556},{'A','F',703},{'A','G',521},{'B','G',391},{'B','H',230},{'B','I',356},{'B','J',220},{'C','F',642},{'C','E',337},{'D','F',829},{'D','K',334},{'E','F',581},{'E','G',1254},{'F','G',887},{'G','H',242},{'H','I',249},{'I','J',713},{'J','K',398}};//边及权值
int Count=0;//记可走边的总数
STNODE Stack;//存放已访问过
SANode Store_Arc_Ver;//存放弧的信息及顶点信息
int LAV=-1,ALL=0;
int Short_Len=1000000,Short_Load=0;//存放最断最路经
void CreateGraph(Graph **G);//创建图
int LocateVer(Graph G,VertexType v);//查找顶点v在图中的位置
void ShowAdjInfo(Graph *G);//查看邻接点信息
int FirstAdjVer(Graph *G,int v,ArcBox **u);//第一邻接点
int NextAdjVer(Graph *G,int v,int w,ArcBox **u);//下一邻接点
void NAV(ArcBox *p,int *n,int v,int w,ArcBox **u);//递归查找下一邻接点
void InitArcBox_mark(ArcBox *p);//初始化mark的值
void DFSTraverse(Graph *G);//深度优先遍历图
void DFST(Graph *G,int v);//剃归深度优先遍历
void InitStack(void);//初始化栈
void Push(VertexType c);//数据进栈
void Pop(void);//出栈
Status IsAdj(int *len,VertexType v);//判断栈顶的点是否与A为邻接点
int main() {
    Graph *G=NULL;
    CreateGraph(&G);
    printf("顶点的邻接表：\n");
    ShowAdjInfo(G);printf("\n\n");
    printf("可走路径结果:\n");
    DFSTraverse(G);printf("\n");
    printf("可走路径总数:%d条；最短路径为:路径%d，长度为:%d\n\n",ALL,Short_Load,Short_Len);
    return 0;
}
void CreateGraph(Graph **G)//创建图 {
    int i,j,k,w;
    char v1,v2;
    ArcBox *pnew;
    (*G)=(Graph *)malloc(1*sizeof(Graph));
    if((*G)==NULL)
    {
        printf("动态内存分配失败，程序终止！\n");
        exit(-1);
    }
    (*G)->arcnum=MAX_ARC_NUM;
    (*G)->vernum=MAX_VER_NUM;
    for(i=0;i<(*G)->vernum;i++)
    {
        (*G)->vertexs[i].data='A'+i;
        (*G)->vertexs[i].firstedge=NULL;
    }
    for(k=0;k<(*G)->arcnum;k++)
    {
        v1=Data[k].v1;
        v2=Data[k].v2;
        w=Data[k].weight;
        i=LocateVer((**G),v1);
        j=LocateVer((**G),v2);
        if(i>=0&&j>=0)
        {
            pnew=(ArcBox *)malloc(1*sizeof(ArcBox));
            if(pnew==NULL)
            {
                printf("动态内存分配失败，程序终止！\n");
                exit(-1);
            }            
            pnew->iver=i;
            pnew->jver=j;
            pnew->weight=w;
            pnew->mark=FALSE;
            pnew->ilink=(*G)->vertexs[i].firstedge;
            pnew->jlink=(*G)->vertexs[j].firstedge;
            (*G)->vertexs[i].firstedge=pnew;
            (*G)->vertexs[j].firstedge=pnew;
        }
        else
        {
            printf("注意：*****顶点%c不存在！*****\n",i<0?v1:v2);
        }
    }
    return;
}
int LocateVer(Graph G,VertexType v)//查找顶点v在图中的位置 {
    int i,result=-1;
    for(i=0;ivernum;v++)
    {
        printf("[%d|%c]",v,G->vertexs[v].data);
        for(w=FirstAdjVer(G,v,&u);w>=0;w=NextAdjVer(G,v,w,&u))
        {
            printf("->[%d|%c|%d]",w,G->vertexs[w].data,u->weight);
        }
        InitArcBox_mark(G->vertexs[v].firstedge);
        printf("\n");
    }
}
int FirstAdjVer(Graph *G,int v,ArcBox **u)//第一邻接点 {
    int w=-1;
    ArcBox *p;
    p=G->vertexs[v].firstedge;
    (*u)=p;
    if(v==p->iver)
    {
        w=p->jver;
        p->mark=TRUE;
    }
    else if(v==p->jver)
    {
        w=p->iver;
        p->mark=TRUE;
    }
    return w;
}
int NextAdjVer(Graph *G,int v,int w,ArcBox **u)//下一邻接点 {
    int n=-1;
    ArcBox *p;
    (*u)=NULL;
    p=G->vertexs[v].firstedge;
    NAV(p,&n,v,w,&(*u));
    return n;
 
}
void NAV(ArcBox *p,int *n,int v,int w,ArcBox **u)//递归查找下一邻接点 {
    if(p->mark==FALSE && (p->iver==v ||p->jver==v))
    {
        (*u)=p;
        if(p->iver==v)
        {
            *n=p->jver;p->mark=TRUE;
        }
        else if(p->jver==v)
        {
            *n=p->iver;p->mark=TRUE;
        }
        else printf("下一邻接点数据出错，请检查！\n");
    }
    else
    {
        if(p->ilink!=NULL && *n==-1)
        {
            NAV(p->ilink,n,v,w,&(*u));
        }
        if(p->jlink!=NULL && *n==-1)
        {
            NAV(p->jlink,n,v,w,&(*u));
        }
    }
    return;
}
void InitArcBox_mark(ArcBox *p)//初始化mark的值 {
    p->mark=FALSE;
    if(p->ilink!=NULL)
    {
        InitArcBox_mark(p->ilink);
    }
    if(p->jlink!=NULL)
    {
        InitArcBox_mark(p->jlink);
    }
    return;
}
void DFSTraverse(Graph *G)//深度优先遍历图 {
    int v;
    for(v=0;vvernum;v++)
    {
        Visited[v]=FALSE;
        InitArcBox_mark(G->vertexs[v].firstedge);
    }
    InitStack();
    DFST(G,0);        
    return;
}
void DFST(Graph *G,int v)//剃归深度优先遍历 {
    int w=-1,flag=1,i=0,enter=1,len=0;
    ArcBox *u;//邻接点
    StackData *p;
    Visited[v]=TRUE;
    Count++;
    Push(G->vertexs[v].data);
    if(Count==11&&IsAdj(&len,Stack.ptop->data)==1) 
    {        
        ALL++;
        printf("路径%-2d：",ALL);
        printf("A");
        p=Stack.ptop;
        len=len+p->lenght;
        if(Short_Len>len) Short_Load=ALL,Short_Len=len;        
        while(p!=Stack.pbottom)
        {
            printf("->%c",p->data);
            p=p->pnext;
        }
        printf(" 总长度为：%d",len);
        printf("\n");
    }
    for(w=FirstAdjVer(G,v,&u);w>=0;w=NextAdjVer(G,v,w,&u))
    {
        enter=1;
        for(i=0;i<=LAV;i++)
        {
            if(Store_Arc_Ver.p[i]==u)
            {
                enter=0;
                break;
            }
        }
        if(enter==1)
        {
            Store_Arc_Ver.p[++LAV]=u;
            Store_Arc_Ver.v_num[LAV]=v;
        }
        if(Visited[w]==FALSE)
        {    
            DFST(G,w);
            Visited[w]=FALSE;
            Count--;
            Pop();
        }
    }
    for(LAV;Store_Arc_Ver.v_num[LAV]==v&&LAV>=0;)//还原当前顶点边的状态并出栈
    {
        Store_Arc_Ver.p[LAV]->mark=FALSE;
        Store_Arc_Ver.p[LAV]=NULL;
        LAV--;
    }
}
void InitStack(void)//初始化栈 {
    Stack.pbottom=Stack.ptop=(StackData *)malloc(1*sizeof(StackData));
    Stack.pbottom->pnext=NULL;
    return;
}
void Push(VertexType c)//数据进栈 {
    StackData *pnew;
    char v1,v2;
    int i;
    pnew=(StackData *)malloc(1*sizeof(StackData));
    pnew->data=c;
    if(c=='A')
    {
        pnew->lenght=0;
    }
    else
    {
        v1=c;
        v2=Stack.ptop->data;
        for(i=0;ilenght=Stack.ptop->lenght+Data[i].weight;
            }
        }
    }
    pnew->pnext=Stack.ptop;
    Stack.ptop=pnew;
    return;
}
void Pop(void)
{
    StackData *p;
    p=Stack.ptop;
    Stack.ptop=p->pnext;
    free(p);
}
Status IsAdj(int *len,VertexType v)//判断是栈顶的点是否与A为邻接点
{
    int i;
    for(i=0;i

C++代码

#include#include#include#include#include#include#include#include#include#include#include#include#include#define max(a,b) (a>b?a:b)
using namespace std;
typedef long long(LL);
typedef unsigned long long(ULL);
const double eps(1e-8);
 
char B[1<<15],*S=B,*T=B,ch;
#define getc() (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++)
int aa,bb; int F() {
      while(ch=getc(),(ch<'0'||ch>'9')&&ch!='-'); ch=='-'?aa=bb=0:(aa=ch-'0',bb=1);
      while(ch=getc(),ch>='0'&&ch<='9')aa=aa*10+ch-'0'; return bb?aa:-aa;
}
#define N 100010
int n,swp,cnt,z[N]; long long ans;
#define swap(a,b) (swp=a,a=b,b=swp)
#define abs(x) (x>0?x:-(x))
#define max(a,b) (a>b?a:b)
#define cmax(x) (ans<(const="" p&a,const="" p&b)="" {return="" a.nx<<2];="" e="" to,v,nxt;}="" e[n<<1];="" gf(int="" x)="" ufs[x]="=x?x:ufs[x]=gf(ufs[x]);}" void="" adde(int="" x,int="" y,int="" v)="" e[++et]="(E)" {y,v,la[x]},la[x]="et;" {x,v,la[y]},la[y]="et;" public:="" graph()="" {et="1;}" add(int="" {d[++tot]="(D)" {x,y,v};}="" make()="" std::sort(d+1,d+1+tot);="" for(int="" i="1;" i<="n;" i++)ufs[i]="i;" cnt="n;" i++)="" if((x="gf(d[i].x))!=(y=gf(d[i].y)))" adde(d[i].x,d[i].y,d[i].v);="" g;="" x,n;}="" d[n];="" d&a,const="" d&b)="" a.x<="cnt;" f="0;">0; t-=t&-t)
            if(z[t]&&(f==0||p[z[t]].x+p[z[t]].y>p[f].x+p[f].y))f=z[t];
      return f;
}
void work() {
      for(int i=1; i<=n; i++)p[i].nx=p[i].x-p[i].y,p[i].ny=p[i].y;
      std::sort(p+1,p+1+n);
      for(int i=1; i<=n; i++)d[i]=(D) {p[i].ny,i};
      std::sort(d+1,d+1+n); d[n+1].x=d[n].x; cnt=1;
      for(int i=1; i<=n; i++)
      {
            p[d[i].n].ny=cnt;
            if(d[i].x!=d[i+1].x)cnt++;
      }
      memset(z,0,sizeof(z));
      for(int i=1,j; i<=n; ins(i++))
            if(j=query(i))G.add(p[i].id,p[j].id,dis(i,j));
}
int main() {
      n=F();
      for(int i=1; i<=n; i++)p[i]=(P) {F(),F(),i}; work();
      for(int i=1; i<=n; i++)swap(p[i].x,p[i].y); work();
      for(int i=1; i<=n; i++)p[i].y=-p[i].y; work();
      for(int i=1; i<=n; i++)swap(p[i].x,p[i].y); work(); G.make();
      printf("%lld\n",ans);
}
/* * this code is made by crazyacking * Verdict: Accepted * Submission Date: 2015-09-11-15.31 * Time: 0MS * Memory: 137KB */