运算律

　　实数和虚数的积等于零

　　实数和实数的和等于实数

　　虚数和虚数的和等于虚数

　　实数加虚数等于合数

　　交换律　

　　交换律是被普遍使用的一个数学名词，意指能改变某物的顺序而不改变其最终结果。交换律是大多数数学分支中的基本性质，而且许多的数学证明需要倚靠交换律。简单运算的交换律许久都被假定存在，且没有给定其一特定的名称，直到19世纪，数学家开始形式化数学理论

　　给定集合S上的二元计算，如果对S中的任意a,b满足

　　a·b = b·a

　　则称·满足交换律。

　　例：

　　1.在四则运算中，加法和乘法都满足交换律。在小学课本中的表述如下：

　　加法交换律:两个数相加,交换加数的位置,它们的和不变.a+b=b+a

　　乘法交换律:两个数相乘,交换因数的位置,它们的积不变.a*b=b*a

　　2.在集合运算中，集合的交，并，对称差等运算都满足交换律。

　　结合律　

　　给定一个集合S上的二元运算·，如果对于S中的任意a,b,c。有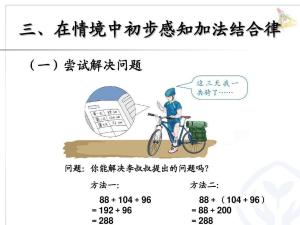：结合律

　　a·(b·c) = (a·b)·c

　　则称运算·满足结合律。

　　例：

　　1.在常见的四则运算中：加法和乘法都满足结合律。在小学课本中表述如下：

　　加法结合律:三个数相加,先把前面两个数相加,再加第三个数,或者先把后面两个数相加,再和第一个数相加,它们的和不变.

　　乘法结合律:三个数相乘,先把前面两个数相乘,再乘第三个数,或者先把后面两个数相乘,再和第一个数相乘,它们的积不变.

　　2.在集合运算中：集合的交，并运算都满足结合律。

　　3.矩阵乘法满足结合律。一个A x B的矩阵乘以一个B x C的矩阵将得到一个A x C的矩阵，时间复杂度为A x B x C。

　　分配律　

　　【定义】给定集合S上的两个二元运算·和*，若它们满足：对任意S中的a,b,c有

　　c·(a*b) = (c·a)*(c·b) 则称运算·对运算*满足左分配律。

　　(a*b)·c = (a·c)*(b·c) 则称运算·对运算*满足右分配律。

　　如果同时满足上面两条，则称运算·对运算*满足分配律。

　　【示例】

　　1.在常见的四则运算中：

　　1)乘法对加法和减法都满足分配律（即同时满足左右分配律）。

　　在小学课本里这个性质被表述为：两个数的和与一个数相乘,可以把两个加数分别与这个数相乘,再把两个积相加。

　　2)除法对加法和减法满足右分配律。（这个事实很少被提到，但的确是对的）

　　2.在集合运算中：

　　1)交运算对并运算满足分配律；

　　2)并运算对交运算满足分配律；

　　3)交运算对差运算满足分配律；

　　4)并运算对差运算满足分配律；等等...

　　公式导引：

　　加法交换律：a+b=b+a

　　乘法交换律：a×b=b×a

　　加法结合律：a+b+c=(a+b)+c=a+(b+c)

　　乘法结合律：(a×b)×c=a×(b×c)

　　左分配律：c·(a*b) = (c·a)*(c·b)

　　右分配律：(a*b)·c = (a·c)*(b·c)