- 阿达马不等式

阿达马不等式
中文名
阿达马不等式
简介
矩阵的子行列式满足的不等式
所属学科
数学
基本介绍
对欧氏空间中任意s个向量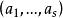 ,必有
,必有
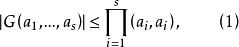 而等号成立的充要条件是:
而等号成立的充要条件是: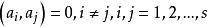 。也即
。也即 两两正交。(1)式称为广义阿达马不等式。
两两正交。(1)式称为广义阿达马不等式。
之所以称(1)式为广义阿达马不等式,是因为n阶实方阵A=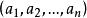 的n个列可以看作带有内积
的n个列可以看作带有内积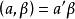 的实数域R上的
的实数域R上的
n维列向量R(n)(即欧氏空间R(n))中的n个列向量,而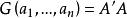 ,故得
,故得
 (其中
(其中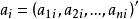 ),这就是通常的阿达马不等式。
),这就是通常的阿达马不等式。
不等式(2)有以下几何意义:
平行多面体的体积不超过两个互补“面”的体积的乘积,而等于这一乘积的充分必要条件是这些“面”互相正交或者在乘积中至少有一个体积等于零。
相关介绍
设 是欧氏空间V中任意s个向量,下述s阶阵
是欧氏空间V中任意s个向量,下述s阶阵
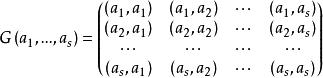 为
为 的格兰姆矩阵。称
的格兰姆矩阵。称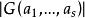 为
为 的格兰姆行列式。
的格兰姆行列式。
格兰姆矩阵是个有广泛应用的矩阵,它有如下的基本结论:
定理1欧氏空间V中向量 的格兰姆矩阵
的格兰姆矩阵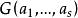 必是半正定阵,而
必是半正定阵,而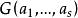 是正定阵的充要条件是
是正定阵的充要条件是 线性无关。
线性无关。
证明当 线性无关时,作线性包L(
线性无关时,作线性包L( ),则它对V的内积来说仍是一个欧氏空间,而
),则它对V的内积来说仍是一个欧氏空间,而 是L(
是L( )的基,故
)的基,故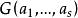 是度量矩阵,因而
是度量矩阵,因而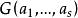 是正定阵。故
是正定阵。故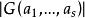 >0。
>0。
当 线性相关,例如
线性相关,例如![]() 是
是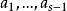 的线性组合:
的线性组合: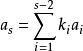 ,将
,将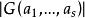 的第s列减去第1列的k1倍、第2列的k2倍、…,第s-1列的ks-1倍,并应用内积的线性性质可得
的第s列减去第1列的k1倍、第2列的k2倍、…,第s-1列的ks-1倍,并应用内积的线性性质可得
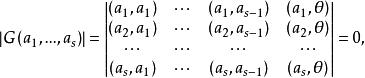
(因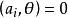 ;i=1,2,…,s)。
;i=1,2,…,s)。
根据上述两点,对任意s个向量 ,恒有:
,恒有: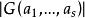 ≥0。但因
≥0。但因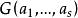 的任何k阶主子阵显然也是格兰姆矩阵,故它的行列式不小于零,所以
的任何k阶主子阵显然也是格兰姆矩阵,故它的行列式不小于零,所以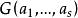 是半正定阵。再由上述两点知,
是半正定阵。再由上述两点知,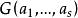 是正定阵的充要条件是,
是正定阵的充要条件是, 线性无关。
线性无关。
由定理1的证明过程,可得推论1及广义阿达马不等式。
推论1欧氏空间V的任意s个向量 的格兰姆行列式
的格兰姆行列式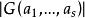 ≥0,而等号成立的充要条件是,
≥0,而等号成立的充要条件是, 线性相关。
线性相关。
由于格兰姆矩阵的半正定(正定性),使我们可以充分运用半正定阵与正定阵的理论去得到更多有用的结论。例如,由正定阵行列式的不等式估计式显然可得广义阿达马不等式。

相关百科
-
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-10-12 17:50:21 查看详情 -
马自达3经典款钜惠13000元 车展钜惠
2025-10-12 17:50:21 查看详情 -
有望在5月底上市 全新宝马X5
2025-10-12 17:50:21 查看详情 -
广汽本田全新皓影正式上市 宝马1系M运动曜熠版上市
2025-10-12 17:50:21 查看详情 -
雪佛兰开拓者正式上市 全新宝马7系/i7正式上市
2025-10-12 17:50:21 查看详情 -
珠海英菲尼迪Q50L优惠达5.4万 成都新宝马3系优惠5万元
2025-10-12 17:50:21 查看详情 -
成都新宝马3系优惠5万元 再送装潢礼包
2025-10-12 17:50:21 查看详情 -
运良版牧马人战马上市 4月15日正式上市
2025-10-12 17:50:21 查看详情 -
德阳马自达6最高优惠3.7万元 最低多少钱
2025-10-12 17:50:21 查看详情 -
上海购金刚最高优惠1.3万 成都海马普力马现金优惠4千元
2025-10-12 17:50:21 查看详情


 求购
求购

