道路

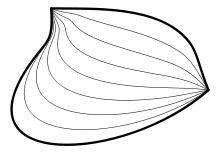两条道路之间的同伦。

道路与环路是代数拓扑分支中同伦论的重要研究课题。道路的同伦就是保持端点不动的道路的连续形变的直观想法的精确化。

明确地说，X 中道路的同伦是一族道路 ft : I → X 使得

ft(0) = x0 与 ft(1) = x1 不变。

由 F(s, t) = ft(s) 定义的映射 F : I × I → X 是连续的。

由一个同伦连接的道路 f0 与 f1 称为同伦的。可以类似地定义保持基点不动的环路的同伦。

同伦的性质定义了拓扑空间中道路的一个等价关系。道路 f 在这个等价关系下的等价类称为 f 的同伦类，通常记作 [f]。

可以将道路以明显的方式复合起来。假设 f 是从 x 到 y 的一条道路，g 是从 y 到 z 的一条道路。道路 fg 定义为首先通过 f 然后通过 g：

显然道路复合只对 f 的终点与 g 的起点重合有定义。如果考虑所有以 x0 为基点的环路，则道路复合是一个二元运算。

道路复合，无论是对一般道路还是环路定义，都不是结合的，因为有不同的参数化。但是在同伦的层次上是结合的，即  [(fg)h] = [f(gh)]。道路复合定义了以 x0 ∈ X 为基点的环路的同伦类上的一个群结构，所得的群称为 X 在以 x0 为基点的基本群，通常记作 π1(X,x0)，这个群一般不可交换。

有一个有时很有用的范畴描述。任何拓扑空间 X 给出了一个范畴其对象是 X 中的点，态射是道路的同伦类。因为这个范畴中任意态射是同构态射，故这个范畴是一个群胚，称为 X 的基本群胚。这个范畴中的环路是自同态（事实上所有都是自同构）。点  x0 ∈ X 的自同构群恰好是以 x 为基点的基本群。基本群的重要定理塞弗特－范坎彭（Seifert–van Kampen）定理在基本群胚的框架下有简明的描述与推广。