黎曼积分

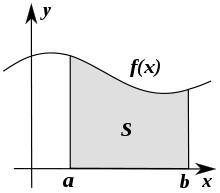作为曲线与坐标轴所夹面积的黎曼积分

对于一在区间上之给定非负函数，我们想要确定所代表的曲线与坐标轴所夹图形的面积，我们可以将此记为

黎曼积分的核心思想就是试图通过无限逼近来确定这个积分值。同时请注意，如取负值，则相应的面积值亦取负值。

一个闭区间的一个分割P是指在此区间中取一个有限的点列。每个闭区间叫做一个子区间。定义为这些子区间长度的最大值：，其中。

再定义取样分割。一个闭区间的一个取样分割是指在进行分割后，于每一个子区间中取出一点。的定义同上。

精细化分割：设以及构成了闭区间的一个取样分割，和是另一个分割。如果对于任意，都存在使得，并存在使得，那么就把分割：、称作分割、的一个精细化分割。简单来说，就是说后一个分割是在前一个分割的基础上添加一些分点和标记。

于是我们可以在此区间的所有取样分割中定义一个偏序关系，称作“精细”。如果一个分割是另外一个分割的精细化分割，就说前者比后者更“精细”。

对一个在闭区间有定义的实值函数，关于取样分割、的黎曼和（积分和）定义为以下和式：

和式中的每一项是子区间长度与在处的函数值的乘积。直观地说，就是以标记点到X轴的距离为高，以分割的子区间为长的矩形的面积。

不太严格地来说，黎曼积分就是当分割越来越“精细”的时候，黎曼和趋向的极限。下面的证明中，会对“越来越‘精细’”作出严格的定义。

要使得“越来越‘精细’”有效，需要把趋于0。如此中的函数值才会与接近，矩形面积的和与“曲线下方”的面积的差也会越来越小。实际上，这就是黎曼积分定义的大概描述。

严格定义如下：是函数在闭区间上的黎曼积分，当且仅当对于任意的，都存在，使得对于任意的取样分割、，只要它的子区间长度最大值，就有：

也就是说，对于一个函数，如果在闭区间上，无论怎样进行取样分割，只要它的子区间长度最大值足够小，函数的黎曼和都会趋向于一个确定的值，那么在闭区间上的黎曼积分存在，并且定义为黎曼和的极限，这时候称函数为黎曼可积的。

这个定义的缺陷是没有可操作性，因为要检验所有的取样分割是难以做到的。下面引进另一个定义，然后证明它们是等价的。

另一个定义: 是函数在闭区间上的黎曼积分，当且仅当对于任意的，都存在一个取样分割、，使得对于任何比其“精细”的分割 and ，都有：

这两个定义是等价的。如果有一个满足了其中一个定义，那么它也满足另一个。首先，如果有一个满足第一个定义，那么只需要在子区间长度最大值的分割中任取一个。对于比其精细的分割，子区间长度最大值显然也会小于，于是满足

其次证明满足第二个定义的也满足第一个定义。首先引进达布积分的概念，第二个定义和达布积分的定义是等价的，具体见达布积分。其次我们证明达布积分的定义满足第一个定义。任选一个分割使得它的上达布和与下达布和都与相差不超过。令等于，其中和是在上的上确界和下确界。再令是和中的较小者。可以看出，当一个分割的子区间长度最大值小于时，关于它的黎曼和与上达布和或下达布和至多相差，所以和至多相差。

由于以上原因，黎曼积分通常被定义为达布积分（即第二个定义），因为达布积分比黎曼积分更简单、更有可操作性。

线性性：黎曼积分是线性变换，也就是说，如果和在区间上黎曼可积，和是常数，则：

由于一个函数的黎曼积分是一个实数，因此在固定了一个区间后，将一个黎曼可积的函数设到其黎曼积分的映射是所有黎曼可积的函数空间上的一个线性泛函。

正定性：如果函数在区间上几乎处处（勒贝格测度意义上）大于等于0，那么它在上的积分也大于等于零。如果在区间上几乎处处大于等于0，并且它在上的积分等于0，那么几乎处处为0。

可加性：如果函数在区间和上都可积，那么在区间上也可积，并且有

无论a、b、c之间的大小关系如何，以上关系式都成立。

上的实函数是黎曼可积的，当且仅当它是有界和几乎处处连续的。

如果上的实函数是黎曼可积的，则它是勒贝格可积的。

如果是上的一个一致收敛序列，其极限为，那么：

如果一个实函数在区间上是单调的，则它是黎曼可积的，因为其中不连续的点集是可数集。

黎曼积分可推广到值属于维空间的函数。积分是线性定义的，即如果，则。特别地，由于复数是实数向量空间，故值为复数的函数也可定义积分。

黎曼积分只定义在有界区间上，扩展到无界区间并不方便。可能最简单的扩展是通过极限来定义积分，即如同反常积分（improper integral）一样。我们可以令

不幸的是，这并不是很合适。平移不变性（如果把一个函数向左或向右平移，它的黎曼积分应该保持不变）丧失了。例如，令若，，若。则对所有

.

但如果我们将向右平移一个单位得到，则对所有，我们得到

.

由于这是不可接受的，我们可以尝试定义：

此时，如果尝试对上面的积分，我们得到，因为我们先使用了极限。如果使用相反的极限顺序，我们得到。

这同样也是不可接受的，我们要求积分存在且与积分顺序无关。即使这满足，依然不是我们想要的，因为黎曼积分与一致极限不再具有可交换性。例如，令在上，其它域上等于0。对所有，。但一致收敛于0，因此的积分是0。因此。即使这是正确的值，可看出对于极限与普通积分可交换的重要准则对反常积分不适用。这限制了黎曼积分的应用。

一个更好的途径是抛弃黎曼积分而采用勒贝格积分。虽然勒贝格积分是黎曼积分的扩展这点看上去并不是显而易见，但不难证明每个黎曼可积函数都是勒贝格可积的，并且当二者都有定义时积分值也是一致的。

事实上黎曼积分的一个直接扩展是Henstock–Kurzweil积分。

扩展黎曼积分的另一种途径是替换黎曼累加定义中的因子，粗略地说，这给出另一种意义上长度间距的积分。这是黎曼-斯蒂尔切斯积分所采用的方法。