完全解析函数

若函数在区域内解析，且区域的边界上每一点都是它的奇点，则它就不能越过区域的任意一部分边界解析开拓；若在上有正则点，则此函数就可以越过边界解析开拓出去。对于开拓后得到的函数及区域，还可以再研究它能否进一步解析开拓，这样就可以不断地解析开拓，一直到不能开拓为止。为了刻画这个事实，需要引进完全解析函数的概念。^[1]

设所有标准元素集合由任一元素 P 沿所有若尔当曲线作解析开拓而得到，此曲线起点在元素 P 的圆心，且对此曲线可以作解析开拓，则称这个标准元素集合为完全解析函数。我们指出，完全解析函数的概念不依赖于初始元素 P 的选择。实际上，设 Q 是由初始元素 P 确定的完全解析函数的任一其他元素，这表示 Q 是由 P 沿着某条曲线开拓得出的。于是 P 可以由 Q 沿曲线开拓得出。如果两个完全解析函数至少有一个共同元素，则这两个函数被认为是相等的。^[2]

一个完全解析函数是一个一般解析函数，它包含其任一元素的所有解析开拓，的定义域称为它的存在区域，的边界称为的自然边界。^[3]

定理内容：属于完全解析函数的诸元素收敛圆的并集构成一个区域。

证明：设 D 是这个并集，它作为诸开集的并集是一个开集，即如果，则是某一元素的收敛圆，且。设 a 与 b 是集 D 的任意两点，则可求出两个元素，使得a 与 b 是它们的圆心。这两个元素是沿某一路线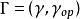互为解析开拓而得出的，这条路线是连结点 a 与 b 而成的。显然，因此 D 是连通开集，即一个区域，它称为完全解析函数的自然定义域或它的存在域。

我们指出，完全解析函数不能是区域 D 内广义的函数，因为它不是单值的。

定理内容：完全解析函数含有不多于圆心在一定点处的可数多个不同元素。

证明：设完全解析函数由圆心在点 a 处的初始元素确定，z 是完全解析函数定义域 D 中的任意一点。设是完全解析函数的一个元素，圆心在点 z 处，它可由元素用圆心在点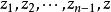的有限元素链得出，其中每后一个元素都是前一元素的直接解析开拓。不是一般性，可以设诸点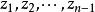有有理坐标。实际上，首先设圆心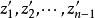是任意的。在点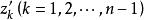的任意小的领域内取一个带有理坐标的点，并用元素代替，根据沿路线解析开拓关于路线同伦形变的不变性定理，在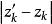充分小时，按新链开拓的结果和按旧链开拓的结果相同。具有元素有理圆心的元素直接解析开拓集合是可数的，恰好与元素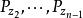的可数集一样。给定与点 z 就唯一地确定了元素，因此不同元素的个数不超过可数集。^[2]

注意：研究完全解析函数的概念，不一定只利用标准元素，可以取任意元素，把完全解析函数看作是解析元素集合，其中 a 取遍某一指标集，这时元素中的每一个元素可由任意其他元素解析开拓得出。^[2]

完全解析函数定义域的边界点称为它的奇点。

设是完全解析函数的一个孤立奇点，是定义域 D 内的一个去心邻域。^[2]

如果任一属于的标准元素在沿着某闭路线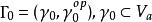作解析开拓时没有改变，则当若当曲线与在内作解析开拓得出的任一元素，在沿任一路线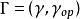开拓时没有改变。

注意：由该引理可推出，在内沿着与同伦的路线解析开拓不改变元素，这样的路线被收缩为任一元素的圆内路线，沿这些路线的解析开拓不改变元素。^[2]

单/多值特征的奇点

设是完全解析函数的孤立奇点，是此点在定义域内的去心邻域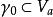，是包围点的闭若当曲线，于是，如果：

（1）沿曲线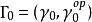绕行将得到初始元素，则称为单值特征的奇点；

（2）沿绕行得到不同初始元素的元素，则称为多值特征的奇点或支点。

n-1阶/无穷阶支点

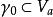设是完全解析函数的支点，是包围点的闭若尔当曲线，于是，如果：

（1）存在这样一个整数，使次同方向绕行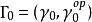得到初始元素，并且是具有上述性质的所有整数中的最小值，则称为阶支点；

（2）若不存在（1）中所述的整数，即同方向绕行得出新而又新的元素，则称为无穷阶阶支点或对数支点。^[2]

注意：容易检验，如果把曲线换为内与同伦的任一若尔当曲线，则支点的阶数不变。^[2]