- 有理曲线

有理曲线
简介
有理曲线是为了统一表示自由曲线和圆锥曲线而发展起来的,它与普通Bezier曲线,B-Spline曲线一样,是一种逼近形式,有很好的几何直观性,通过对控制顶点的调整,即可实现对曲线形状的控制,同时有理曲线上每个顶点上的权因子又为形状控制提供了新的自由度。综合使用以权因子为基础的方法和以控制顶点为基础的方法可以对曲线形状进行更为直观、快速准确的控制,在飞机、轮船、汽车等复杂外形产品的几何设计中有实用价值。[1]
定义
表述一
在代数曲线中,其上的点的坐标可用一个参数的有理函数表示的曲线,称为有理曲线。已经证明,多重点至多为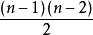 个的n次代数曲线是有理曲线。例如,代数曲线
个的n次代数曲线是有理曲线。例如,代数曲线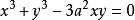 是以
是以![]() 为参数由
为参数由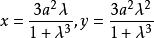 表示的有理曲线。[2]
表示的有理曲线。[2]
表述二
亏格式0的代数曲线就是有理曲线。[3]
相关定理
定理一
射影直线![]() 是有理曲线。
是有理曲线。
证明:![]() 的函数域
的函数域![]() ,则
,则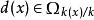 。
。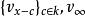 是
是![]() 的全部标准离散赋值。设其对应的赋值环为
的全部标准离散赋值。设其对应的赋值环为![]() 和
和![]() ,则
,则![]() 是
是![]() 的极大理想的生成元,
的极大理想的生成元,![]() 是
是![]() 的极大理想的生成元。因
的极大理想的生成元。因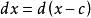 对所有的
对所有的![]() 成立,因此
成立,因此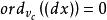 对所有的
对所有的![]() 成立。又因
成立。又因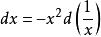 ,得
,得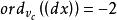 ,故有
,故有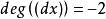 ,因此
,因此![]() 的亏格为零。
的亏格为零。
定理二
设X 是光滑的射影曲线,则X同构于![]() ,当且仅当存在X上两个不同点P,Q相互线性等价。
,当且仅当存在X上两个不同点P,Q相互线性等价。
证明:设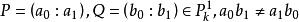 ,则
,则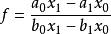 是
是![]() 上的非平凡的有理函数,
上的非平凡的有理函数,![]() 和
和![]() 分别是
分别是![]() 的单零点和单极点,且
的单零点和单极点,且![]() 在
在![]() 没有其他零点和极点。因此,
没有其他零点和极点。因此,![]() 线性等价于
线性等价于![]() 。
。
反之设X上两个线性等价点![]() ,
,![]() ,则存在
,则存在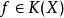 ,使
,使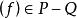 。于是
。于是![]() 是一个有限扩张,令
是一个有限扩张,令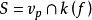 ,则
,则![]() 是
是![]() 的一个离散赋值环,并且
的一个离散赋值环,并且![]() 是
是![]() 的极大理想的生成元,故点
的极大理想的生成元,故点![]() 在
在![]() 之上的分歧指数
之上的分歧指数![]() 。由于
。由于![]() 是
是![]() 在
在![]() 中的唯一的扩张,故有
中的唯一的扩张,故有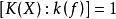 ,即
,即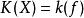 。
。
定理三
有理曲线同构于射影直线![]() 。
。
证明:设 X 是有理曲线,P 是 X 上任意一点,则由R-emann-Roch定理得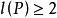 ,因此存在
,因此存在![]() 与
与![]() 线性等价,根据定理二可得X 与射影直线
线性等价,根据定理二可得X 与射影直线![]() 同构。[3]
同构。[3]
定理四(Luroth定理)
设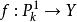 是从有理曲线到光滑射影曲线
是从有理曲线到光滑射影曲线![]() 上的一个态射,假定
上的一个态射,假定![]() 所诱导的函数域扩张
所诱导的函数域扩张![]() 是可分的,则
是可分的,则![]() 是有理曲线。
是有理曲线。
证明:设n是![]() 的次数,则根据Hurwitz公式有
的次数,则根据Hurwitz公式有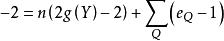 ,因
,因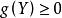 ,
,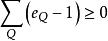 ,故
,故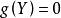 。[3]
。[3]



 求购
求购








