- 共轭数

共轭数
定义
如果 ,用
,用![]() 代替
代替![]() 中的
中的![]() 所得到的数
所得到的数![]() 叫做
叫做![]() 的共轭数,注意当且仅当
的共轭数,注意当且仅当![]() 是实数时,
是实数时,![]() 。[2]
。[2]
相关性质定理
定理1
两个复数之和的共轭数等于这两个数的共轭数之和,两个复数之积的共轭数等于每个因数的共轭数之积。
例如:如果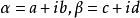 ,那么
,那么
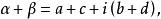
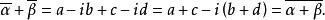 同样
同样
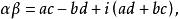 如同
如同![]() 与
与![]() 的对应(写作
的对应(写作![]() ),既在加法中又在乘法中被保持,叫做自同构,实数域没有自同构,除了每个数对应于它自己的这种平凡的情况,而复数域除了自己对应于自己和共轭关系的对应外,也没有自同构。数学专业的大学毕业生将会一再遇到这个概念。
),既在加法中又在乘法中被保持,叫做自同构,实数域没有自同构,除了每个数对应于它自己的这种平凡的情况,而复数域除了自己对应于自己和共轭关系的对应外,也没有自同构。数学专业的大学毕业生将会一再遇到这个概念。
定理2
如果![]() 具有实系数且
具有实系数且![]() 是一个复数, 那么
是一个复数, 那么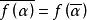 。[2]
。[2]
令
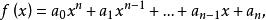 其中的
其中的![]() 都是实数,从而
都是实数,从而![]() ,又
,又
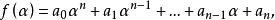 于是由定理1,
于是由定理1,
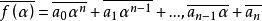
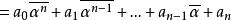
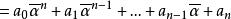
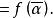
定理3
![]() 设是一个复系数多项式,而令
设是一个复系数多项式,而令![]() 为每一个系数用它的共轭数代替后得到的多项式,那么
为每一个系数用它的共轭数代替后得到的多项式,那么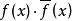 是一个实系数多项式。
是一个实系数多项式。
如果
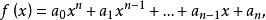 那么,
那么,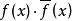 中
中![]() 的系数为
的系数为
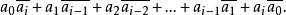 对于
对于![]() ,有
,有![]() ,由于它等于它自己的共轭数,所以是实数。
,由于它等于它自己的共轭数,所以是实数。
定理4
如果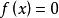 具有实系数,且有一个根
具有实系数,且有一个根![]() ,那么
,那么![]() 也是它的根。
也是它的根。
因为如果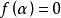 ,那么
,那么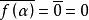 ,所以
,所以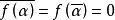 。
。
由于只有当![]() 是实数的时候,才有
是实数的时候,才有![]() ,我们得到下面定理。
,我们得到下面定理。
定理5
一个实系数方程的非实根成共轭对出现。
令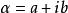 ,那么
,那么
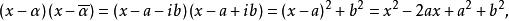 其系数都是实的,这样,如果一个n次实系数多项式
其系数都是实的,这样,如果一个n次实系数多项式![]() 有一个非实根,那么
有一个非实根,那么![]() 可写成一个实的二次因式和另一个
可写成一个实的二次因式和另一个![]() 次实系数因式的积,继续这样论证下去证得下面定理。
次实系数因式的积,继续这样论证下去证得下面定理。
定理6
每一个实系数多项式可以写成若干个一次的或二次的实系数多项式的积。[2]
主要有两类共轭数
共轭无理数:形如a+√b和a-√b的,a、b为有理数,但b不是完全平方数的数互称为共轭无理数。
共轭复数:复数范围内,实部相同,虚部符号相反的,形如a+bi和a-bi的两数互称为共轭复数数。
以上两种共称为共轭数。

-
“数”说上汽大众全新朗境 报价降价
2025-09-29 13:27:27 查看详情 -
“数”说上汽大众全新朗境 欢迎品鉴
2025-09-29 13:27:27 查看详情 -
“数”说上汽大众全新朗境 有现车销售
2025-09-29 13:27:27 查看详情 -
“数”说上汽大众全新朗境 现车销售
2025-09-29 13:27:27 查看详情 -
“数”说上汽大众全新朗境 最新怎么样
2025-09-29 13:27:27 查看详情


 求购
求购





