波特图

波特图是由贝尔实验室的荷兰裔科学家亨德里克·韦德·波特在1930年发明。波特用简单但准确的方法绘制增益及相位的图，因此他发明的图也就称为波特图。

波特图幅频图的频率用对数尺度表示，增益部分一般都用功率的分贝值来表示，也就是将增益取对数后再乘以20。由于增益用对数来表示，因此一传递函数乘以一常数，在波特增益图只需将图形的纵向移动即可，二传递函数的相乘，在波特幅频图就变成图形的相加。幅频图纵轴0分贝以下具有正增益裕度、属稳定区，反之属不稳定区：

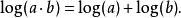
波特图相频图的频率也用对数尺度表示，而相位部分的单位一般会使用度。配合波特相频图可以估算一信号进入系统后，输出信号及原始信号的比例关系及相位。例如一个Asin(ωt) 的信号进入系统后振幅变原来的k倍，相位落后原信号Φ，则其输出信号则为(Ak)sin(ωt−Φ)，其中的k和Φ都是频率的函数。相频图纵轴-180度以上具有正相位裕度、属稳定区，反之属不稳定区

若将系统的增益以复数表示，则复数增益取对数后的虚部即为相位，因此二传递函数的相乘，在波特相位图上也是图形的相加。^[1]

波特图可用来计算负反馈系统的增益裕度（gain margin）及相位裕度，进而确认系统的稳定性。^[2]

先定义以下的符号：

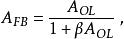
其中

• A_FB是考虑反馈时的放大器增益（闭环增益）
• β是反馈系数
• A_OL是不考虑反馈时的放大器增益（开环增益）。

在开环增益A_OL远大于1时，闭环增益A_FB可以用以下方式近似

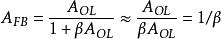
在开环增益A_OL远小于1时，闭环增益A_FB可以用以下方式近似

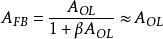
增益A_OL是频率的复变函数，有大小及相位。

上述的式子中，若βA_OL乘积=−1时，可能会出现增益无穷大（即为不稳定）的情形。（若用大小和相位来表示，此时βA的大小为1，相位为-180度，此条件即称为巴克豪森稳定性准则。配合波特图，不但可以判断系统是否稳定，也可以判断系统接近以上不稳定条件的程度。

在判断系统稳定性时，会用到以下二个频率。第一个频率f₁₈₀是上述乘积相位恰为-180度的频率，第二个频率f_0dB则为乘积的绝对值|βA_OL|=1时的频率（若以分贝表示时，则为0dB）。频率f₁₈₀可以用下式来计算：

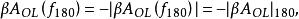
其中| |表示复数的绝对值（例如|a+jb| = [a+b]）。而频率f_0dB有以下的关系：

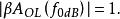
增益裕度（gain margin, GM）是衡量系统稳定程度的一种方法。在波特相位图上可以找到βA_OL相位到达-180度时的频率，该频率即为f₁₈₀，之后就可以在增益图上找到该频率时βA_OL的大小。

若|βA_OL|₁₈₀> 1，表示此系统不稳定。若|βA_OL|₁₈₀< 1，此系统稳定，而|βA_OL|分贝值和0dB（对应增益大小为1）的距离表示系统距离不稳定的程度，称为增益裕度。

增益裕度也可以用下式表示：

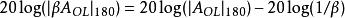
相位裕度（phase margin, PM）是另一种衡量系统稳定程度的方法。在波特增益图上可以找到|βA_OL|大小为1的频率，该频率即为f_0dB，之后就可以在相位图上找到该频率时βA_OL的相位。

若βA_OL(f_0dB) 的相位 > −180°，表示在任何频率时系统都会稳定，因为在f₁₈₀时大小已小于1，f_0dB时的相位和-180度之间的差称为相位裕度。

若只是单纯要判断系统是否稳定，在系统为最小相位系统时，若以下的式子成立，则系统稳定：

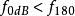
若是非最小相位系统，需要用其他方式判断稳定性，如奈奎斯特图。^[1]

波特分析仪（Bode plotter）是一种类似示波器的仪器，可以量测反馈控制系统或滤波器在各频率的增益及相位变化，绘制成波特图。波特测试仪可以量测系统的截止频率、增益裕度及相位裕度，在分析或测试系统的稳定性时很有帮助。

波特分析仪的功能和网络分析仪一样，不过网络分析仪一般会用来分析相当高频时的系统特性。

在教育或研究的应用上，利用波特分析仪绘制特定传递函数的波特图也可助于了解该系统的特性。^[2]