- 莫比乌斯反演
莫比乌斯反演
中文名
莫比乌斯反演公式
适用领域范围
数论
提出者
奥古斯特·费迪南德·莫比乌斯
莫比乌斯反演的引入
莫比乌斯反演是数论中的重要内容，在许多情况下能够简化运算。我们考虑以下求和函数：
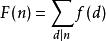
我们需要找到
和
之间的关系。从和函数定义当中，我们可以知道：
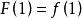
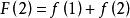
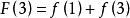
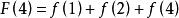
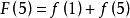
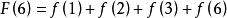
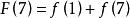
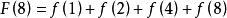
那么：
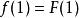
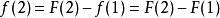
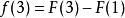
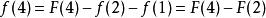
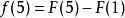
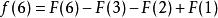
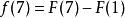
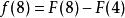
从中，可以看出，若
(
为质数)那么，
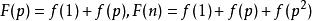，所以，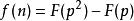
.
如果我们要让函数满足：
那么通过以上推导，我们可以知道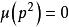
，所以我们作出以下猜测：
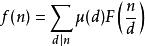
莫比乌斯反演定理
设
和
是定义在正整数集合上的两个函数,定义如下。
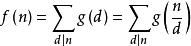
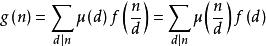则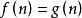
.
莫比乌斯反演定理证明
充分性证明：
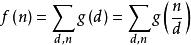
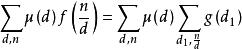
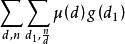
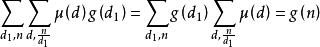
考虑到：
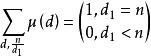因此
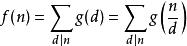
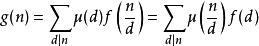
必要性证明：
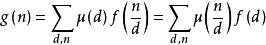
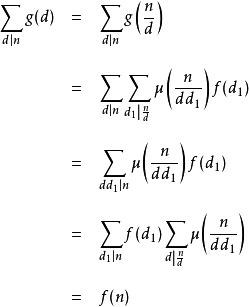
考虑到：
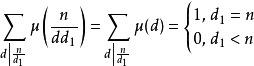
因此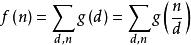
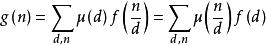
莫比乌斯函数
定义当
时，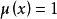
当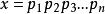
（
为不同的质数，且次数都为1），
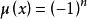
其余情况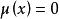
注意，
函数也为积性函数。证明略。
莫比乌斯反演的性质
性质一（莫比乌斯反演公式）：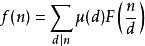
性质二：μ(n)是积性函数
性质三：设f是算术函数，它的和函数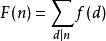
是积性函数，那么f也是积性函数。
相关百科
-
-
-
-
-
-
-
-
玛尔库斯·撒尔维乌斯·奥托
2025-09-21 03:39:37 查看详情 -
-
求购