球体表面积

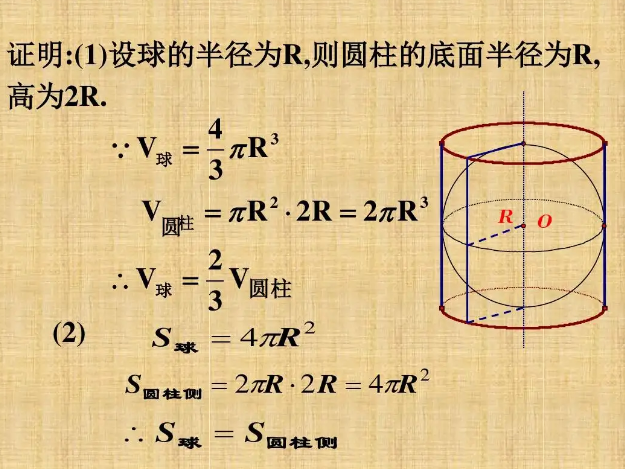球体表面积(3)球体表面积公式S=4πr²=πD²

√表示根号

把一个半径为R的球的上半球横向切成n（无穷大）份， 每份等高

并且把每份看成一个类似圆台，其中半径等于该类似圆台顶面圆半径

则从下到上第k个类似圆台的侧面积 球体表面积S(k)=2πr(k)×h

其中r(k)=√[R^2-﹙kh）^2],

h=R^2/{n√[R^2-﹙kh）^2}.

S(k)=2πr(k)h=(2πR^2)/n则 S=S(1)+S(2)+……+S(n)= 2πR^2;

乘以2就是整个球的表面积 4πR^2;

求体积求导

可以把半径为R的球看成像洋葱剥皮（非纵向或横向，而是环切）一样分成n层，每层厚为

计算公式

计算公式

，半径获得增量时

计算公式

，体积增加的部分的体积就为

计算公式

。 球体表面积

极限的思想：当n趋于无穷大的时候，记此时的半径差为dr，当r增量趋近于零时的增加体积dv。此时球的每层的厚度就薄的像个曲面一样，这部分很薄的体积除以dr就是球的表面积了。

导数定义为：当自变量的增量趋于零时，因变量的增量与自变量的增量之商的 极限。

球的体积为

计算公式

,

计算公式

所以同时求导就可得S(r)=4πr^2, 球体表面积